L’étude de la géométrie de l’espace nécessite des représentations. Mais pour comprendre celles-ci, des éléments de théorie de géométrie de l’espace sont nécessaires…
Il faut donc au démarrage aborder ces deux sujets en parallèle.
Si un matériel concret (baguettes,…) reste indispensable pour travailler dans l’espace, un logiciel comme GeoGebra peut, par son côté dynamique, aider grandement à décoder les représentations. Visualiser une section de cube dans GeoGebra 3D, par exemple, permet de la voir sous différents angles en faisant tourner le cube, ce qui peut s’avérer très utile pour ceux qui “ne voient pas” dans l’espace.
Mais aucun logiciel n’est la panacée. La construction de sections avec crayon et règle, par exemple, garde tout son sens et exige des élèves une réflexion et une habileté technique incontournables.
Le logiciel peut être utile pour faire chercher les élèves ou pour faciliter la correction et les explications en classe.
Dans la première activité, nous avons choisi de commencer par une vision large des sections de cube possibles. Nous proposons de faire travailler les élèves avec GGB 3D, après une réflexion préliminaire. Un soin tout particulier a été apporté à la rédaction de cette première activité afin de permettre à des élèves ne connaissant pas GGB 3D de travailler en quasi-autonomie, même si la présence et un coup de pouce du professeur resteront parfois nécessaires.
La deuxième activité s’intéresse aux types de représentations. Au départ d’images données sur papier, on demande de repérer des familles de droites et leurs propriétés.
La troisième activité approfondit le travail de représentation, en envisageant cette fois des cubes.
Il est temps ensuite de passer aux constructions de sections de cube sur papier à l’activité 4.
Nous retrouvons GGB 3D à l’activité 5 pour une activité plus dynamique sur les sections de cubes.
Une activité de théorisation est à prévoir aussi. Elle peut se faire à plusieurs moments, à choisir par l’enseignant. Nous l’avons placée en fin de document, sous le titre “Faisons le point”.
Les documents destinés aux élèves sont regroupés à la fin de l’article, dans un fichier téléchargeable.
Les débuts de la géométrie de l’espace avec GeoGebra
Présentation des activités
Avant de se lancer dans la technique de construction d’une section de cube, il est utile d’avoir une idée des différentes formes que peut prendre cette section.
Activité 1. Sections de cube
a) Construisez un cube et cherchez toutes les formes possibles de la section de ce cube par un plan. Classez les sections obtenues en les décrivant le plus précisément possible (triangle, trapèze, …). Essayez de ne pas en oublier.
b) En groupes, comparez les listes individuelles pour les compléter si nécessaire.
c) Poursuivez le travail avec le logiciel Geogebra dans le but de vérifier la liste et de la compléter si nécessaire.
Étape 1 : mise en place de la fenêtre Graphique 3D
- dans le menu Affichage, sélectionner Graphique 3D puis fermer la fenêtre Graphique
- enlever les axes de la fenêtre 3D en basculant la Barre de style de la fenêtre Graphique 3D puis en cliquant sur l’icône Afficher ou cacher les axes.
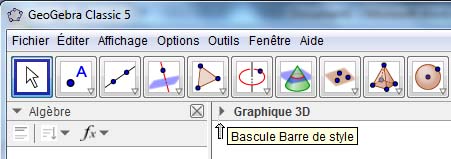
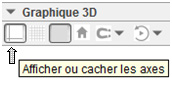
Étape 2 : construction du cube
- dérouler l’icône des solides dans la barre d’outils afin de choisir le cube ;
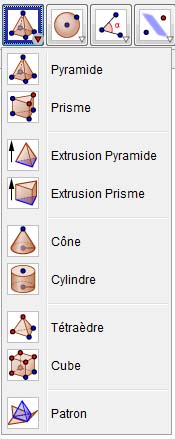
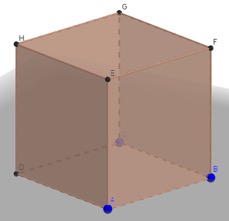
- la sélection de deux points A et B dans le plan affiché est suffisante ;
- dans la fenêtre Algèbre, le cube obtenu est nommé a.
Étape 3 : construction du plan
- dans la barre de saisie, taper Point(a) et valider. Un point, nommé I par le logiciel, est placé sur une arête du cube ;
- activer l’icône Déplacer
 ,
,
- cliquer sur le point I créé et le déplacer sur une autre arête du cube ;
- répéter ces opérations pour placer deux autres points J et K sur des arêtes du cube ;
- pour la construction du plan contenant les points créés, activer l’icône Plan passant par trois points

- puis sélectionner les points I, J et K.
Étape 4 : intersection du cube et du plan
- sélectionner l’icône Intersection de deux surfaces (1), puis cliquer sur le cube (2) et le plan (3) dans la fenêtre Algèbre.
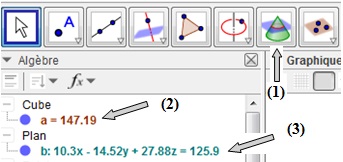
Étape 5 : recherche des sections possibles
- activer l’icône Déplacer ;
- déplacer les points créés I, J et K afin d’obtenir différentes sections du cube par le plan ;
- reproduire soigneusement et au fur et à mesure les situations obtenues sur la feuille fournie par le professeur (un exemple est donné ci-dessous) ;
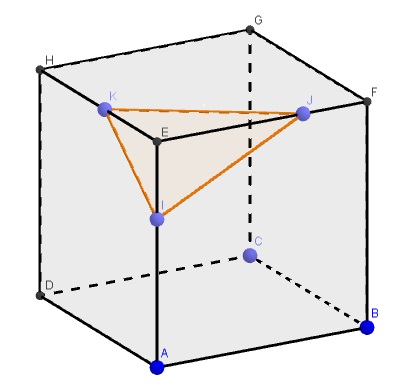
Remettre votre production au professeur à la fin de la séance.
Indications méthodologiques
Cette première activité comporte 4 parties.
La première (a) peut être faite en préparation à domicile.
La deuxième (b) ne devrait pas prendre une heure de cours complète. Cette exploration dans l’espace physique réel aide grandement à décoder les représentations du logiciel.
La troisième (c) prendrait une heure en salle informatique. Si les élèves ont fini avant la fin de l’heure, on peut leur demander de préparer une construction précise pour des cas particuliers (le cas d’un losange par exemple).
La dernière partie, la synthèse devrait prendre une heure maximum.
Dans la feuille de questions, à l’étape 2, un exemple de cube a été mis pour montrer une position qui permet une recherche efficace.
A l’étape 5, un exemple de solution est là pour inciter les élèves à remplir la feuille de solutions au fur et à mesure du travail sans quoi, ils risquent bien de ne pas se souvenir de tous les cas rencontrés à la fin de l’heure.
On peut rendre la section plus visible en réglant l’opacité du cube sur 0 (clic droit sur le cube dans la fenêtre algébrique/ propriétés/ couleur…).
La synthèse en classe se fera idéalement en projetant un fichier GGB, de manière à pouvoir bouger le cube et les sections pour corriger et compléter les productions des élèves.
Un clic droit sur la section permet d’accéder à ses propriétés. On peut alors demander d’en créer une vue 2D en vraie grandeur.
Il est indispensable aussi d’avoir un cube concret et du matériel pour visualiser les sections dans l’espace réel.
Cette première activité permet en outre de découvrir de manière naturelle des propriétés de géométrie de l’espace.
Par exemple, le fait qu’un plan coupant deux plans parallèles les coupe selon des droites parallèles peut émerger lors de la recherche des formes possibles pour les sections (toutes les sections ayant au moins quatre côtés présentent nécessairement une paire de côtés parallèles). Cette propriété peut également apparaître lorsqu’il faut reproduire les sections sur le papier.
Lors de ces activités, le professeur peut collecter les énoncés trouvés par les élèves au fur et à mesure de leurs découvertes.
Plus tard, lors d’une activité de synthèse théorique, le professeur pourra poser des questions pour faire émerger les énoncés non trouvés. Il restera à distinguer définitions, axiomes et propriétés et mettre de l’ordre dans les énoncés pour obtenir une théorie suffisante à ce niveau.
Le relevé détaillé de toutes les sections possibles, les justifications ou constructions précises constituent un prolongement, certes intéressant mais pas indispensable.
Solutions
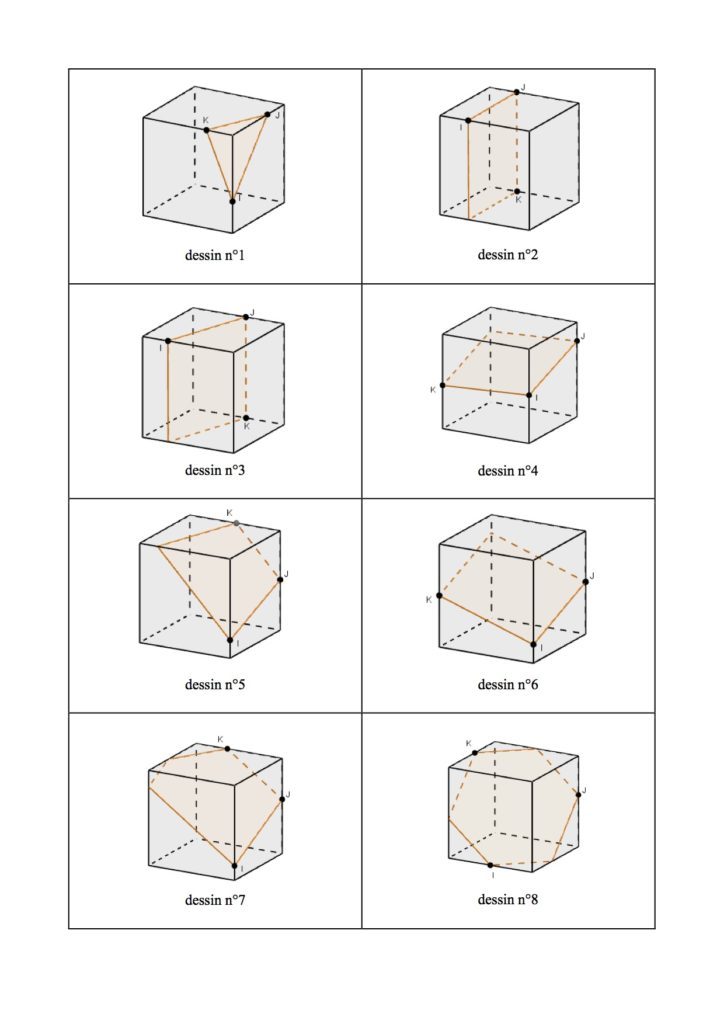
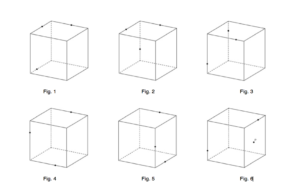
Section en forme de triangle (Fig. 1)
Si le plan de section coupe trois faces entourant un même sommet, la section est nécessairement un triangle.
Suivant la position des points d’intersection des arêtes avec le plan de section, le triangle peut être quelconque, isocèle ou équilatéral mais pas rectangle.
Section en forme de quadrilatère
a) Le plan de section coupe deux paires de faces parallèles.
Le quadrilatère le plus général obtenu dans ce cas est un parallélogramme (Fig. 4). En effet si un plan coupe deux plans parallèles, il les coupe suivant deux droites parallèles entre elles.
On peut avoir le cas particulier d’un losange (Fig. 6), d’un rectangle (Fig. 3) ou d’un carré (Fig. 2)
b) Le plan de section coupe une paire de faces parallèles et deux faces adjacentes.
Le quadrilatère le plus général obtenu dans ce cas est un trapèze (Fig. 5). On peut avoir le cas particulier d’un rectangle ou d’un carré.
Section en forme de pentagone (Fig. 7)
Si le plan coupe cinq faces du cube, il coupe nécessairement deux paires de faces opposées parallèles. Le pentagone obtenu ne peut donc être régulier; il a deux paires de côtés parallèles.
Section en forme d’hexagone (Fig. 8)
Si le plan coupe les six faces du cube, il coupe nécessairement trois paires de faces parallèles. L’hexagone obtenu a donc trois paires de côtés opposés parallèles et peut en particulier être régulier.
La représentation du cube proposée dans l’activité 1 est familière aux élèves et est utilisée spontanément. Néanmoins, les différents types de représentations de situations spatiales ne sont en général pas bien connus et compris. Prendre du recul, en comparant les projections centrale et parallèle est bien utile.
Nous le proposons au départ d’images dans l’activité 2 et ensuite sur des cubes à l’activité 3. La synthèse est établie ensuite.
La représentation du cube proposée dans l’activité 1 est familière aux élèves et est utilisée spontanément. Néanmoins, les différents types de représentations de situations spatiales ne sont en général pas bien connus et compris. Prendre du recul, en comparant les projections centrale et parallèle est bien utile.
Nous le proposons au départ d’images dans l’activité 2 et ensuite sur des cubes à l’activité 3. La synthèse est établie ensuite.
Activité 2. Vers les représentations
Voici des images extraites de différents contextes.
Identifiez sur chaque image des familles de droites présentant une même caractéristique.
Comparez les caractéristiques des familles de droites sur les représentations et dans la réalité.
 |  | |
| Fig.1 | Fig.2 | |
 |  | |
| Fig.3 | Fig.4 |
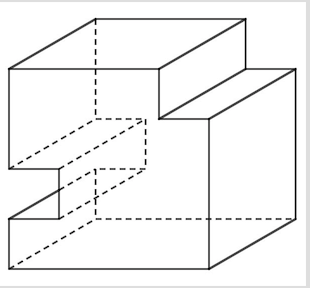
Fig.5
Solution
Rames de métro
Les verticales de la réalité sont représentées par des verticales. Pour les horizontales, il faut distinguer :
– la famille des droites parallèles au front du preneur de photo (on les appelle frontales) dont les représentations sont parallèles entre elles ;
– l’autre famille d’horizontales qui sont représentées par des droites convergeant vers un même point.
Jeu vidéo
Toutes les familles de droites parallèles sont représentées par des familles de droites parallèles.
Estampe
Mêmes constatations que pour le jeu vidéo même si la taille du décor est nettement plus petite.
Bâtiment
Comme pour la première photo, les verticales de la réalité sont représentées par des verticales. On discerne deux familles de droites horizontales parallèles dans la réalité qui sont chacune représentée par des droites convergeant vers un même point. Ces deux points sont situés sur une droite horizontale de l’image.
Pièce d’atelier
Comme pour le jeu vidéo et l’estampe, les familles de droites parallèles sont représentées par des familles de droites parallèles. On a ici le cas particulier d’une famille de parallèles horizontales de l’objet représentées par des horizontales sur le dessin.
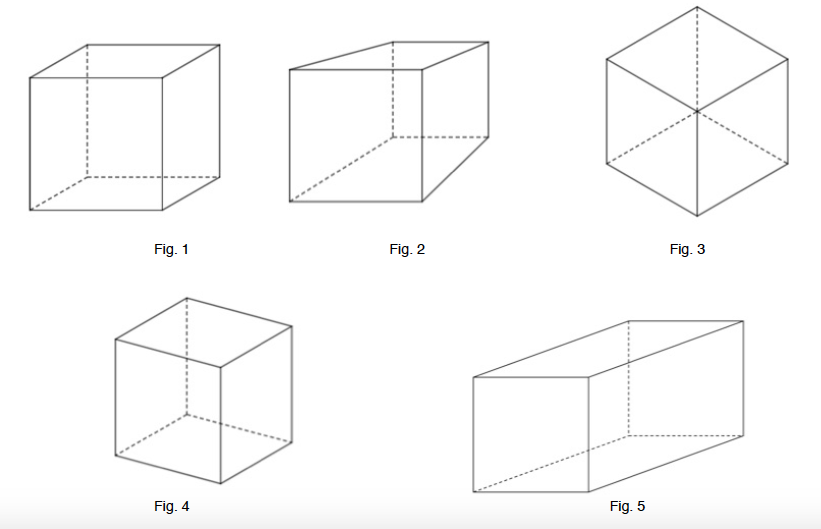
Activité 3. Représentation du cube
a) Retrouvez parmi ces dessins les types de perspectives découvertes lors de l’activité 2.
b) Dans chaque cas, imaginez un deuxième cube identique au premier et situé à l’arrière de celui-ci ; dessinez ses deux faces visibles.
c) Quelle(s) représentation(s) utiliseriez-vous de préférence pour faire des exercices, entre autres des sections ?
Indications méthodologiques
La représentation en projection centrale de la figure 2 n’est là que pour contraster avec celles en projection parallèle. L’important est que les élèves se rendent compte qu’elle n’est pas pratique pour la géométrie car ni le parallélisme ni les rapports de longueurs sur une même direction ne sont conservés. Si on veut terminer la construction de la face latérale du deuxième cube, on peut utiliser les points de fuite de diagonales parallèles.
Cet exercice est l’occasion de prendre du recul par rapport aux représentations du cube./
Solutions
a) Seule la figure 2 correspond à la représentation utilisée pour le métro et le bâtiment. Les familles de droites parallèles dans l’espace ont pour images soit des droites parallèles, soit des droites qui se coupent en un point appelé point de fuite. Ce type de représentation s’obtient par projection sur un plan au départ d’un point (dans la réalité, l’œil, une lampe ou l’objectif d’un appareil photo). Le résultat de cette projection centrale s’appelle perspective à point de fuite.
Dans les quatre autres cas, les parallèles ont des images parallèles, comme dans le jeu, l’estampe et la pièce d’atelier. On peut obtenir ces images par des projections parallèles sur un plan (dans la réalité, l’ombre au soleil).
Le dessin obtenu dépend de la position du cube par rapport au plan de projection et de la direction de projection. Les images par projection parallèle sont également appelées perspectives axonométriques.
– La figure 1 correspond à la représentation utilisée pour la pièce d’atelier : deux faces sont parallèles au plan de projection. Dans ces deux faces, les longueurs et les angles sont conservés. On parle aussi de perspective cavalière dans ce cas particulier de projection parallèle.
– Pour la figure 3, la direction de projection est orthogonale au plan de projection et le cube est positionné avec une diagonale perpendiculaire au plan de projection. Tous les arêtes du cube y sont représentées par des segments de même longueur. C’est pour cette raison que l’on parle ici de perspective isométrique.
– La figure 4 correspond à la représentation utilisée pour le jeu vidéo et l’estampe. On la rencontre souvent : plans de montage de meubles en kit ou de jeux de construction, logos publicitaires, …
– A La figure 5, on “voit” plutôt un parallélépipède rectangle. C’est une perspective cavalière d’un cube, avec une direction de projection “rasante”, comme une ombre au soleil couchant.
b) Si l’ajout de la face latérale droite du cube à l’arrière ne pose pas de problème dans le cas des projections parallèles, il n’en va pas de même dans le cas de la figure 2. Le placement de l’arête verticale arrière n’est pas évident car la longueur du côté fuyant du deuxième cube est inconnue, plus petite que celui du premier.
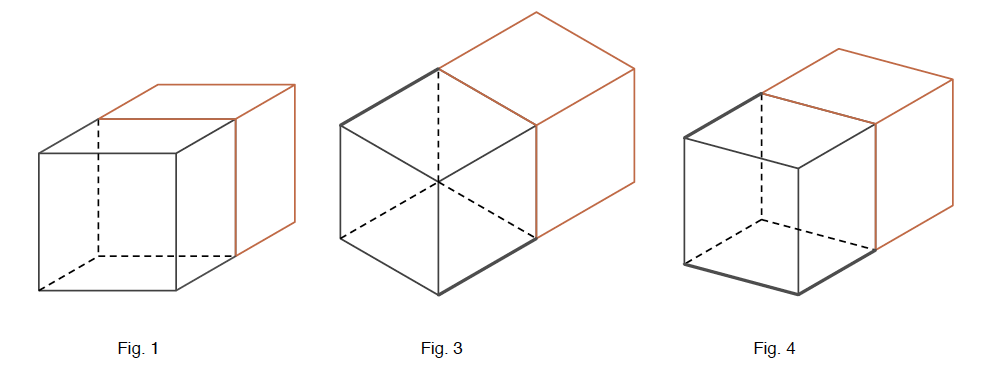
b)
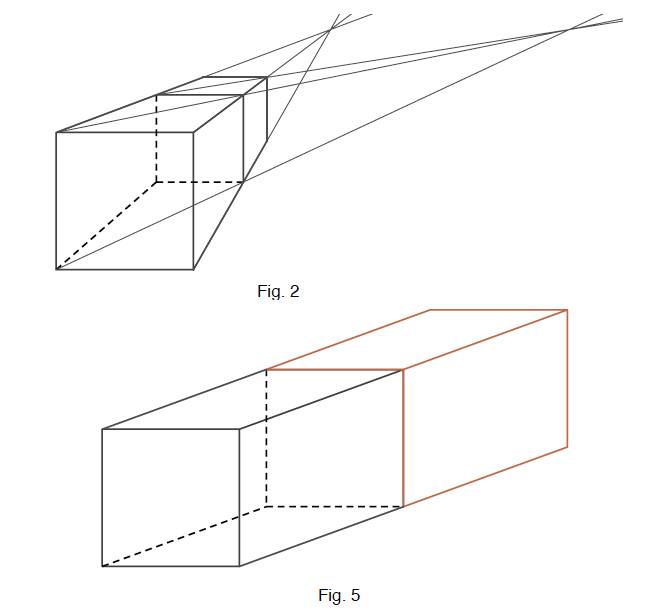
c) Comme une projection parallèle conserve le parallélisme et les rapports de longueur dans chaque direction, elle convient mieux dans le cadre de la géométrie qu’une projection centrale (Fig. 2). Les dessins 1 et 4 sont préférables au 3 qui a deux sommets confondus et au 5 qui fait plus penser à un parallélépipède.
Synthèse des activités 1 à 3
| Projection parallèle | Projection centrale |
| Rayons parallèles | Rayons issus d’un point |
| Résultat : perspective respectant le parallélisme | Résultat : perspective à point de fuite |
La projection centrale est la plus proche de la vision oculaire. Les projections de la plupart des familles de droites parallèles s’y rejoignent en des points appelés points de fuite. Cette projection utilisée en peinture n’est toutefois pas pratique pour l’étude mathématique puisqu’elle ne conserve ni le parallélisme ni les rapports de longueurs. En géométrie, on utilise plutôt la projection parallèle.
Les projections de l’espace sur un plan sont des transformations d’un espace à trois dimensions vers un espace à deux dimensions.
Théorie
Définition d’une projection parallèle
Soient un plan et une droite d non parallèle à .
La projection parallèle d’un point P sur le plan parallèlement à d est l’intersection du plan et de la parallèle à d passant par P.
Propriétés des projections parallèles
– La projection parallèle d’une droite est un point si la droite est parallèle à d, une droite dans tous les autres cas.
– Si deux droites sont parallèles, leurs projections sont parallèles. Attention, la réciproque n’est pas vraie.
– La projection parallèle conserve les rapports de longueurs de segments parallèles.
– Les longueurs des segments parallèles au plan de projection sont conservées.
Activité 4. Sections au crayon
Pour chaque cube, construisez la section par le plan déterminé par les points.
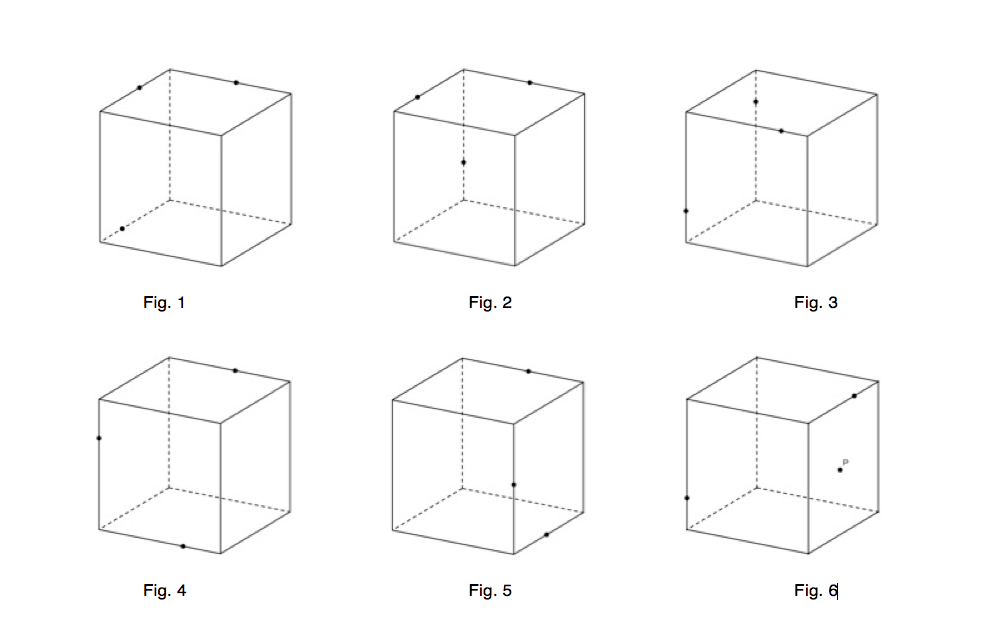
Indications méthodologiques
Il est vraiment utile de demander aux élèves de numéroter dans l’ordre chronologique les traits qu’ils construisent. Cela leur permettra de retrouver plus tard le « film » de la construction de la section.
Il y a parfois plusieurs chemins pour arriver à la section; nous n’en présentons qu’un seul. Dans les solutions proposées, des traits portent un même numéro lorsque l’ordre de construction est indifférent.
Le tracé de parallèles demande de la précision ; la moindre petite déviation a des conséquences importantes. Les élèves doivent bien vérifier à la fin de leurs constructions que les côtés de la section appartenant à des faces opposées sont bien parallèles entre eux. On peut suggérer aux élèves de colorier d’une même teinte les paires de traits parallèles entre eux.
Pour les figures 4 et 5 qui nécessitent des recherches de points de percée, il y a plusieurs choix possibles pour « sortir » du cube.
Solutions
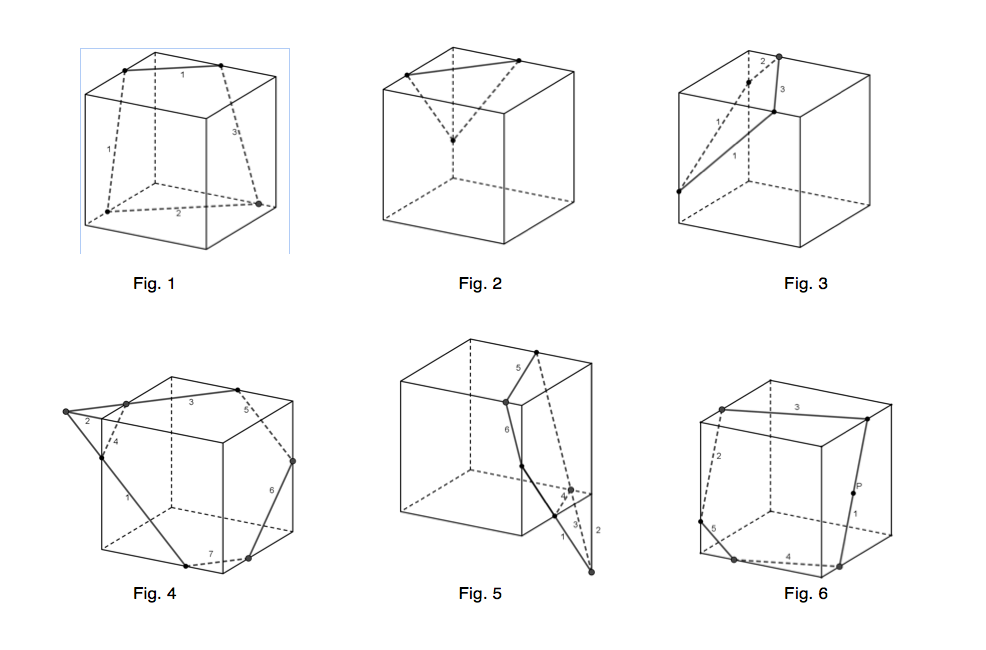
Les constructions s’appuient sur deux propriétés de géométrie de l’espace :
– une droite passant par deux points d’un plan est contenue dans ce plan ;
– deux plans parallèles sont coupés par un troisième plan suivant deux droites parallèles.
Les constructions dans les figures 4 et 5 nécessitent en plus la recherche d’un point de percée d’une droite dans un plan.
Examinons la figure 4. La construction, dans la face arrière, d’une parallèle à la droite de la face avant donne un point dans la face latérale droite mais on ne dispose pas d’un second point dans cette face. L’idée est alors de « sortir du cube » en prolongeant des droites coplanaires jusqu’à leur intersection et de trouver ainsi de nouveaux points à relier.
La figure 6 propose un point P à l’intérieur d’une face plutôt que sur une arête. Comme nous disposons d’un autre point de cette face, nous pouvons les relier. Ici, il ne faut pas oublier la première propriété citée ci-dessus : la droite reliant ces deux points est bien entièrement contenue dans le plan de cette face. Il faut donc prolonger le segment reliant le point supérieur au point P jusqu’à son intersection avec l’arête inférieure et ensuite continuer le processus de construction.
Faisons le point
Les énoncés récoltés jusqu’ici peuvent différer d’une classe à l’autre. Par exemple, on pourrait avoir, dans la liste, les énoncés suivants :
Enoncé 1 : Si deux plans se coupent, ils se coupent selon une droite.
Enoncé 2 : Si deux plans parallèles sont coupés par un troisième, les deux droites d’intersection sont parallèles.
Enoncé 3 : Deux droites sont parallèles si elles sont coplanaires et n’ont pas de point commun.
Le travail de théorisation consiste alors en différentes tâches :
– Corriger les énoncés si nécessaire.
L’énoncé 3 est complété par « ou sont confondues ».
– Les classer les énoncés en définitions, axiomes et théorèmes.
L’énoncé 1 est un fait qu’on a observé mais qu’on ne peut démontrer : c’est un axiome.
L’énoncé 2 peut être démontré par un raisonnement : c’est un théorème.
L’énoncé 3 est une définition.
– Les mettre dans un ordre cohérent et ajouter des énoncés manquants.
L’énoncé 2 parle de droites parallèles et de plans parallèles ; l’énoncé 3 doit donc le précéder et il faudra ajouter aussi la définition de plans parallèles.
Il est illusoire d’espérer de la sorte obtenir plus qu’une ébauche de théorie. Certains énoncés peuvent même avoir des statuts différents selon l’ordre de découverte. Mais cette activité permet aux élèves de « vivre » une construction axiomatique, ce qui est une démarche intellectuelle très riche qui est rarement possible dans les mathématiques du secondaire. Loin de nous l’idée qu’il faille aller très loin dans cette démarche mais elle est instructive, même à ses débuts, pour les élèves.
Au final, on devrait avoir dans la théorie les éléments suivants :
– La détermination des droites et plans.
– Les définitions de droites parallèles, de plans parallèles et de droite parallèle à un plan.
Quelques axiomes.
- Il existe au moins quatre points non coplanaires
- Toutes les propriétés planes sont valables dans tous les plans de l’espace
- Si une droite a deux points dans un plan, elle est entièrement dans le plan.
- Si deux plans se coupent, leur intersection est une droite.
Quelques théorèmes
- Si deux plans parallèles sont coupés par un troisième, les deux droites d’intersection sont parallèles
- Les critères de parallélisme de deux plans et d’une droite et un plan.