Enjeux
Socles 3.2.3 :
– Dégager des régularités, des propriétés, argumenter.
– Dégager les caractéristiques d’une symétrie orthogonale.
De quoi a-t-on besoin ?
– Un miroir par enfant.
– Un grand carré tracé sur une feuille.
– Un grand parallélogramme tracé sur une autre feuille.
– Un crayon et du papier pour garder une trace écrite des observations faites.
Situation 1
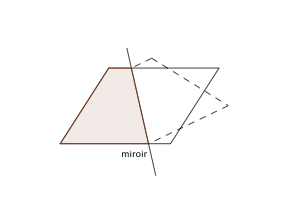
Pose le carré sur ton bureau et place le miroir perpendiculairement à ce carré de sorte qu’il soit séparé en deux morceaux distincts : une partie du carré se reflète dans le miroir et l’autre se trouve derrière le miroir.
– Quelle figure forme l’ensemble constitué du morceau du carré situé devant le miroir et de son image ?
– Quelles figures peux-tu obtenir en déplaçant légèrement le miroir ?
Garde une trace écrite de tes découvertes.
Questions pour aider
– Peux-tu obtenir un triangle, un carré, un rectangle, … ? Si oui, peux-tu en obtenir plusieurs ?
– Peux-tu obtenir des formes qui ont plus que 4 côtés ? Lesquelles ?
– Quelles sont les formes géométriques que tu ne pourras jamais obtenir ?
Solutions
Les solutions diffèrent suivant l’endroit où est déposé le miroir.
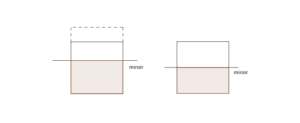
1. La base du miroir coupe deux côtés opposés du carré,
– perpendiculairement à ces côtés : on obtient une famille infinie de rectangles avec le cas particulier du carré initial lorsque le miroir est déposé sur la médiane de ce carré.
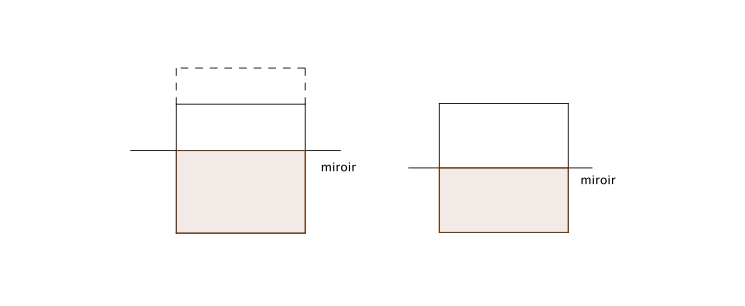
– non perpendiculairement à ces côtés : on obtient une infinité d’hexagones non réguliers, non convexes et admettant 4 angles droits.
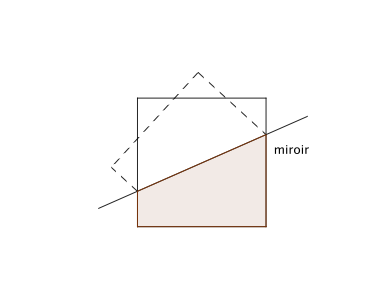
2. La base du miroir coupe deux côtés adjacents, tel que moins de la moitié du carré de départ est placé devant le miroir et y a son reflet;
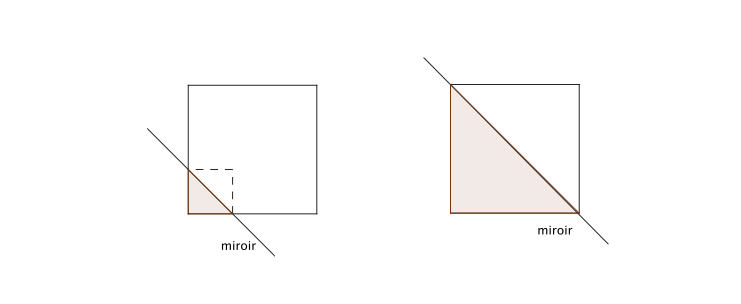
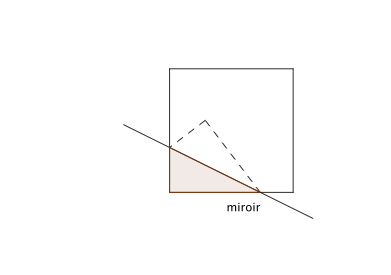
– si les deux segments du carré se reflétant dans le miroir ont la même longueur, la base du miroir est alors parallèle à une diagonale du carré et on obtient une infinité de carrés dont le cas particulier du carré initial si le miroir est déposé sur la diagonale de celui-ci.
– si les deux segments du carré se reflétant dans le miroir sont de longueurs différentes, on obtient une infinité de cerfs-volants qui ont la particularité d’avoir deux angles droits.
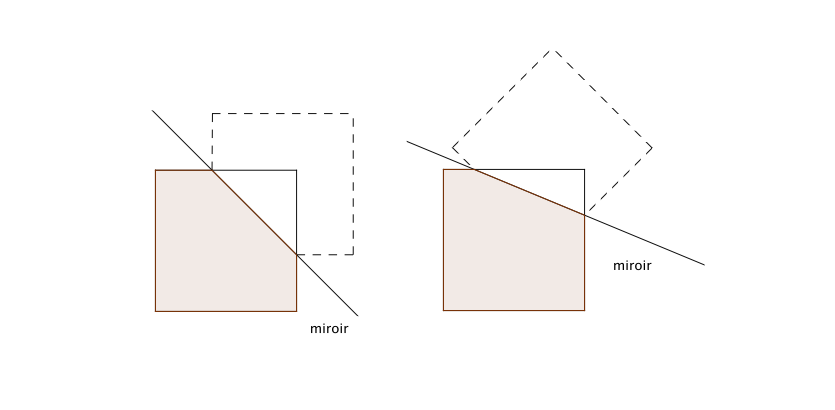
3. La base du miroir coupe deux côtés adjacents, tel que plus de la moitié du carré de départ se reflète dans le miroir, on obtient une infinité d’octogones non réguliers, non convexes, admettant 6 angles droits.
Situation 2
Pose le parallélogramme sur ton bureau et place le miroir perpendiculairement au parallélogramme de sorte qu’il soit séparé en deux morceaux distincts : une partie se reflète dans le miroir et l’autre se trouve derrière le miroir.
– Quelle figure forme l’ensemble constitué du morceau du parallélogramme situé devant le miroir et de son image ?
– Quelles figures peux-tu obtenir en déplaçant légèrement le miroir ?
Garde une trace écrite de tes découvertes.
Solutions
Les solutions diffèrent suivant l’endroit où est déposé le miroir.
1. La base du miroir coupe deux côtés opposés,
– perpendiculairement à ces côtés : on obtient une infinité de trapèzes isocèles et le cas particulier d’un triangle isocèle lorsque le miroir passe par un sommet du parallélogramme.
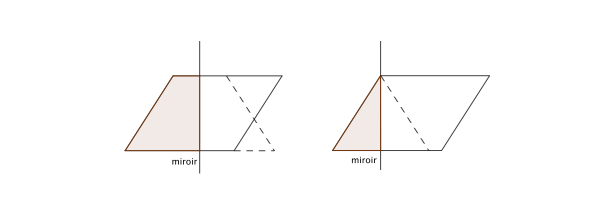
– parallèlement aux deux autres côtés du parallélogramme : on obtient une famille infinie d’hexagones non réguliers et non convexes, ayant trois paires de côtés parallèles.
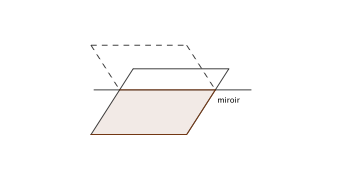
– en position quelconque par rapport aux côtés : on obtient une infinité d’hexagones non réguliers et non convexes.
2. La base du miroir coupe deux côtés adjacents issus d’un angle obtus,
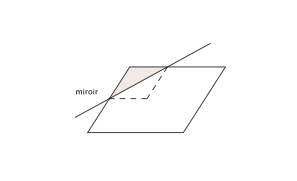
– si les deux morceaux de côtés qui se reflètent dans le miroir ont même longueur : on obtient une infinité de losanges ;
– si les deux morceaux de côtés qui se reflètent dans le miroir sont de longueurs différentes : on obtient une infinité de cerfs-volants.
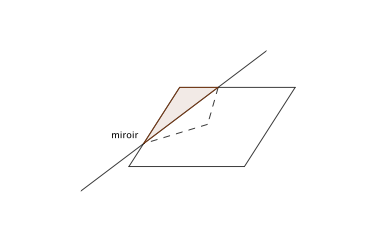
3. La base du miroir coupe deux côtés adjacents, issus d’un angle aigu
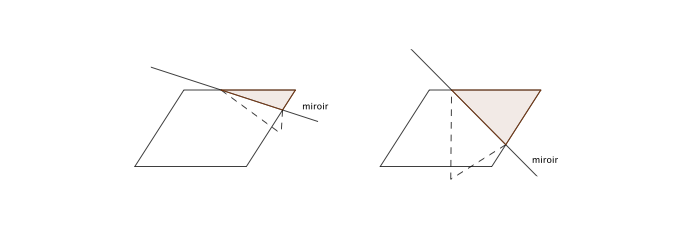
– si les deux morceaux de côtés qui se reflètent dans le miroir ont même longueur : on obtient une infinité de losanges ;
– si les deux morceaux de côtés qui se reflètent dans le miroir sont de longueurs différentes : on obtient une infinité de cerfs-volants convexes ou non convexes (appelés aussi fers de lance) ;
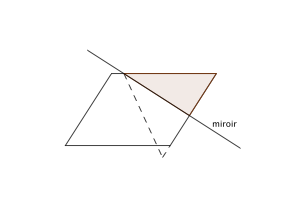
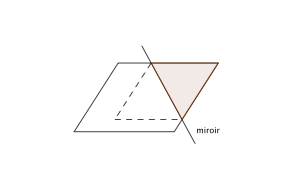
dans le cas particulier où la droite est perpendiculaire à un côté, on obtient une infinité de triangles isocèles.
Si le parallélogramme présente des angles aigus de 60° (et donc obtus de 120°), on peut obtenir des triangles équilatéraux ; si le parallélogramme présente des angles aigus de 45 °, on peut obtenir des triangles rectangles isocèles.
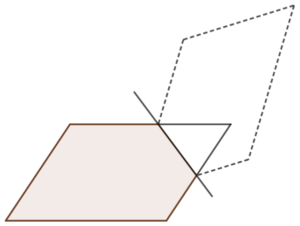
Deux autres possibilités, communiquées par Pascaline Gevers :
- un octogone
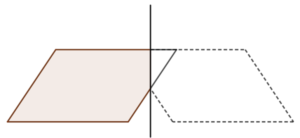
- un heptagone
Prolongements
– Préciser davantage les formes géométriques à obtenir.
– Faire une réflexion sur les formes géométriques impossibles à obtenir.