De quoi s’agit-il ?
Pour devenir expert en connaissance du nombre, il ne suffit pas de dénombrer une collection,
de faire du comptage, de « dire combien il y en a ». Il faut pouvoir faire des liens entre les nombres, entre l’aspect cardinal et ordinal.
La séquence se déroule sur plusieurs activités, chaque activité pouvant être répétée plusieurs fois :
- Activité 1 : JEU DES COLLIERS
- Activité 2 : JEU DES BRACELETS (3D)
- Activité 3 : JEU DES BRACELETS (2D)
- Activité 4 : TROUVER LA PERLE MANQUANTE
Enjeux
(issu du Référentiel des Compétences Initiales)
- Attendus en nombres et opérations (p.56) : reconnaitre globalement et immédiatement des représentations structurées des nombres jusqu’à 6 (ici, représentation du schème du dé).
- Savoir-faire en nombres et opérations (p.57) : s’approprier l’aspect ordinal des nombres. Situer un nombre dans la suite numérique.
- Objectifs généraux en formation mathématique (p.50) : l’enseignant doit donner du sens aux savoirs mathématiques et utiliser, d’une part, ce langage particulier qui permet de décrire, dessiner, structurer l’environnement et, d’autre part, de conserver des traces de la structuration et de l’organisation de la pensée. Dans ce cas-ci, il s’agit d’habituer les élèves à dessiner de manière simplifiée une situation mathématique pour apprendre progressivement l’abstraction. De modéliser pour dégager des notions mathématiques et pour pouvoir les conceptualiser.
ACTIVITÉ 1 : JEU DES COLLIERS
De quoi a-t-on besoin ?
Par élève, un pendentif sur lequel se trouve un schème comme sur le dé (1 à 6) (4 séries de 6 colliers pour 24 enfants, 1 couleur par série). (voir fichier annexé)

Comment s’y prendre ?
Cette activité est reproduite plus d’une fois, avec des consignes de plus en plus subtiles.
Chaque élève reçoit 1 pendentif sur lequel se trouve 1 schème comme sur le dé (1 à 6).
Les enfants circulent dans la salle de gymnastique, la classe ou la cour.
Au signal, des consignes, telles les suivantes, sont données:
- Se grouper par couleur. Pour cette première consigne il n’y a aucun enjeu, il s’agit d’une mise en route afin de s’habituer à l’organisation.
- Se grouper d’après le schème représenté sur son collier : les 1 avec les 1, les 2 avec les 2….
- Tous les enfants portant le schème 4 (par exemple) se mettent à tel endroit, ceux qui ont plus que 4 à un deuxième endroit et ceux qui ont moins que 4 à un troisième endroit.
- Tous ceux qui ont 3 et moins que 3 vont à tel endroit et tous ceux qui ont plus que 3 à un autre.
- Se mettre deux par deux au hasard. Ensuite celui des qui a le plus petit nombre s’accroupit, celui qui a le plus grand nombre lève les mains. L’enseignant fait verbaliser les enfants : « comment sais-tu que tu as plus ? », il fait référence aux précédentes activités de comparaison de collections par correspondance terme à terme.

- Se grouper par couleur, puis dans chaque groupe se ranger dans l’ordre : 1, 2, 3…
(plus facile assis que debout).- Il est important que l’élève trouve sa place dans sa rangée et sente qu’il est bien placé, mais aussi qu’il puisse observer un autre groupe en face. Les enfants peuvent également poser leur pendentif sur leur chaise afin de prendre du recul et voir la suite des nombres.
On vérifie ensuite : le premier enfant se lève, se nomme « 1 », puis le deuxième se lève et se nomme « 2 » (il est le 2ème et il y a 2 enfants debout, l’aspect cardinal et l’aspect ordinal sont reliés).
On compte ainsi de 1 à 6 puis on décompte de 6 à 1.
- La fois suivante demander aux élèves de trouver leur place et de laisser chacun trouver la sienne car certains, plus rapides, ont vite fait de placer leurs compagnons.
Il est essentiel de faire remarquer les relations « +1 » et « -1 » existant entre chacun des nombres placés côte à côte, de faire verbaliser les enfants en posant les questions « Comment sais-tu que tu es à la bonne place ? « , » Pourquoi le 5 est après le 4 ? »
Le «1 de plus» doit primer sur la comptine.
- Il est important que l’élève trouve sa place dans sa rangée et sente qu’il est bien placé, mais aussi qu’il puisse observer un autre groupe en face. Les enfants peuvent également poser leur pendentif sur leur chaise afin de prendre du recul et voir la suite des nombres.
- Une fois les enfants rangés dans l’ordre, on peut également demander :
- à ceux dont la place est à côté du 2 par exemple de lever la main ;
- de se nommer : « je suis le 5, je suis entre le 4 et le 6 »,
ces deux mêmes consignes pouvant ensuite être données sans que les élèves soient rangés ;
- combien d’enfants as-tu à ta droite, y a-t-il des nombres plus petits ? (le 3 a 2 enfants à sa droite, le 4 en a 3… on ne peut évidemment pas demander combien il y en a de l’autre côté car si nous nous arrêtons ici à 6, la suite n’est pas terminée) ;
- ceux qui sont entre le 2 et le 6 s’accroupissent (+ difficile parce qu’il y a plus qu’un nombre entre le 2 et le 6).
- Se ranger par ordre mais indépendamment de la couleur, en trouvant les copains qui permettent de créer une série, même s’ils n’ont pas la même couleur.
- Se mettre par deux et se serrer la main si on est voisin (par exemple le 2 et le 3 peuvent se serrer la main : « nous sommes voisins, l’un de nous deux a «juste 1 de plus »)
Variante : se serrer la main quand on croise un « voisin qui a 1 de plus ou 1 de moins ».

À un moment dans l’activité on peut proposer aux enfants qui se débrouillent bien avec leur nombre d’échanger leur collier avec un copain (pour ne pas représenter toujours le même nombre).
Suite à cette activité, les élèves sont amenés à dessiner (avec des lunettes mathématiques)
la situation qu’ils ont vécue[1]. Les dessins sont ensuite commentés et analysés (objectivement) en groupe classe. Dans ce cas-ci, la discussion a mis en évidence que ce que l’on cherche à représenter ce sont les nombres et non les enfants (c’est un cours de math). Après l’échange, les élèves sont invités à redessiner la situation en s’appuyant sur les bonnes idées de leurs « collègues ».
Échos d’une classe
Exemple de premier jet :




Exemple de deuxième jet :

Certains élèves, plus rapides, ont tendance à indiquer aux autres leur place (ou à les placer), il a donc fallu ajouter la consigne supplémentaire de laisser les autres chercher à leur rythme…quitte à se tromper. De toute façon, une vérification est faite en « lisant » les pendentifs : on se réfère alors à la litanie.
Lors de la deuxième séance de l’activité 1, le temps de distribuer les colliers, les premiers étaient déjà installés à leur (bonne ) place. J’avais préparé des chaises, ce qui est plus facile que si les enfants doivent rester debout et immobiles le temps des explications. J’ai volontairement ajouté une septième chaise, les élèves n’ont pas été perturbés et ont laissé la septième vide.
Commentaires
Un travail sur la reconnaissance des différents schèmes est utile avant cette activité.
On peut relier ces activités en donnant, par exemple, un sachet de 3 jetons à l’enfant qui porte le pendentif 3. Il est alors possible de poser les jetons sur le schème du pendentif. Il faut ajouter un jeton de plus pour l’enfant qui a le schème 4, et encore un jeton de plus pour celui qui a le schème 5…
L’invariance du nombre et la correspondance terme à terme sont des prérequis.
ACTIVITÉ 2 : JEU DES BRACELETS (3D)
De quoi a-t-on besoin ?
Un « bracelet » avec des perles cubiques. Sur l’une des faces de chaque perle a été dessiné un schème du dé, les perles sont mises dans l’ordre numérique.
Un dé et des jetons pour compter les points.

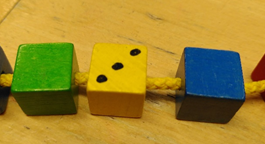
Comment s’y prendre ?
L’enjeu de l’activité est que les élèves mémorisent la place des nombres les uns par rapport aux autres.
Préparation du jeu
Les enfants sont placés par deux, un bracelet devant eux. Les schèmes sont cachés pour le moment.
Les nombres sont rangés dans l’ordre croissant de gauche à droite, lors de la deuxième séance on peut placer les bracelets verticalement.
Le but du jeu consiste à retourner la perle selon la consigne, il faut donc mémoriser leur place.On tire au sort pour savoir qui commence.
Déroulement du jeu
L’’enseignante lance le dé, sans le montrer aux élèves et dit le nombre affiché, par exemple, le 6. Le premier des deux joueurs retourne une perle. S’il s’agit de la bonne, il reçoit un point (il peut prendre un jeton-témoin). Le dé apporte un côté ludique mais pas indispensable, il est aussi intéressant pour l’enseignant de proposer des nombres selon une stratégie.
L’enseignante invite les élèves à mémoriser le schème dessiné sur la perle ainsi que sa place dans le bracelet. L’enseignant verbalise : le 6 est à l’extrémité droite, c’est la dernière perle. Les élèves qui n’avaient pas trouvé la bonne perle peuvent faire apparaitre le 6, puis la perle est à nouveau retournée.
C’est le tour du deuxième joueur de retourner une perle, l’enseignante relance le dé et nomme le 4, par exemple. Les élèves cherchent, verbalisent, visualisent, mémorisent. Et ainsi de suite jusqu’à ce que les élèves retournent aisément et directement chaque bonne perle.
Chaque fois, l’enseignant verbalise ou fait verbaliser la place du schème : le 2 est sur la deuxième perle juste à côté du 1, les 3 et 4 sont plutôt au milieu et sont l’un à côté de l’autre, le 6 est la dernière perle à droite, le 5 est l’avant-dernière perle juste à côté du 6…
Après quelques essais, les enfants sont invités à partager leurs stratégies,
ils mettent ainsi des mots sur l’ordre des nombres, et pour appuyer cela ils peuvent retourner toutes les perles du bracelet en une fois.
Ensuite (ou lors d’une autre séance) les élèves changeront de place pour appréhender le caractère permanent de l’ordre des nombres et pour ne pas associer les nombres aux couleurs des perles.
Les duos changeront également car si l’élève peut apprendre de son compagnon, il n’est pas agréable d’être toujours le « perdant ». Si on réunit les élèves qui ont perdu au premier jeu, à la fin de la deuxième partie, il n’y aura qu’un quart des élèves qui auront perdu les deux fois…
Échos d’une classe
- Certains duos ont spontanément coopéré.
- Les élèves étaient placés par duos de même niveau.
Commentaires
- En prérequis on aura appris à se situer dans l’espace et travaillé le vocabulaire spatial.
On fera également référence aux repères gauche/droite affichés en classe. - On peut expliquer aux enfants qu’en mathématique, on range souvent les nombres de gauche à droite, du plus petit au plus grand.
ACTIVITÉ 3 : LE JEU DES BRACELETS (2D)
De quoi a-t-on besoin ?
Pour chaque élève un bracelet représenté sur feuille cartonnée (cf. annexe) et 6 bouchons. Ce bracelet deviendra référent dans l’étape suivante.


Comment s’y prendre ?
Si le côté ludique est très motivant pour les enfants, nous allons progressivement nous en éloigner pour un petit peu plus d’abstraction. De même, si l’activité en duo peut apporter des échanges entre enfants, chacun doit finalement faire ses propres apprentissages.
Les élèves ont devant eux une bandelette sur laquelle est représenté un bracelet.


Les schèmes sont cachés à l’avance.
Comme lors du jeu précédent, l’enseignant lance le dé et chaque élève est invité à soulever un et un seul bouchon puis à le replacer. Ici l’élève est en compétition avec lui-même et l’enseignante insiste pour que les enfants retiennent la place de chaque schème comme précédemment.
Le jeton-témoin obtenu en cas de réussite ajoute un côté ludique et permet aisément à l’enseignant de repérer les élèves qui ont plus de difficultés.
On peut aussi demander aux enfants de désigner les nombre voisins de celui dont le jeton a été soulevé.

Échos d’une classe
J’ai choisi de mettre des bouchons d’une seule couleur par enfant pour éviter l’association nombre/couleur.
ACTIVITÉ 4 : TROUVER LA PERLE MANQUANTE
De quoi a-t-on besoin ?
Les portions de bracelets et les schèmes isolés (cf. annexe).
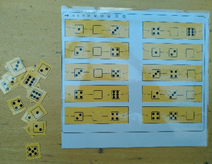
Comment s’y prendre ?
Cette fois il s’agira de retrouver un nombre sur une suite incomplète.
Les élèves auront devant eux une série de « morceaux » de bracelets ainsi que des étiquettes portant chacune un schème. Ils devront déposer le bon schème sur la perle vide. La vérification se fait aisément par l’élève en plaçant la bandelette-référent (bandelette de l’activité 3) juste au-dessus.
Cinq séries différentes de dix morceaux de bracelet ont été prévues, la quantité de séries faites sera fonction du rythme de chacun.



Commentaires
Il est utile lors des activités 2 et 3 de rappeler aux enfants que, même lorsqu’on joue, c’est pour apprendre et de leur expliquer qu’il s’agit ici de visualiser les nombres et d’apprendre à voir dans sa tête les relations entre les nombres.
Échos d’une classe
Prolongements
Il faut avoir une bonne notion de la cardinalité car le passage du cardinal à l’ordinal est la plus grande preuve de souplesse mentale. L’enfant en difficulté peut aller revoir la bandelette complète posée à distance, la mettre en mémoire et revenir à sa place.
Au départ les bracelets à compléter étaient séparés mais cela posait un problème de l’orientation de gauche à droite, j’ai donc donné une feuille munie d’un repère avec les bracelets placés les uns sous les autres, ce qui peut poser problème de clarté à l’un ou l’autre enfant.
Donc je donne des bracelets individuels et en quantité restreinte à ceux qui ont des difficultés.

- Dans la bandelette-référent, on peut mettre des taches sur certains nombres.
- On peut remplacer le schème du dé par d’autres schèmes, d’autres représentations, puis par des chiffres.
- On peut encore demander aux enfants de trouver l’erreur dans une suite de nombres.
- En 1ère primaire l’activité des bouchons peut être exploitée pour l’addition : « soulevez deux bouchons pour faire 7 ». On pourra comparer les propositions : 1 et 6, 2 et 5.
- En 1ère primaire on peut utiliser l’écriture chiffrée.
Vers où cela va-t-il ?
- La connaissance des nombres jusqu’à 6 puis au-delà.
- Il est possible de faire le même genre de travail avec des nombres plus grands, cacher les nombres du tableau de 100 avec des bouchons par exemple.
Commentaires
Dans la séquence, on effectue un va-et-vient régulier entre l’aspect cardinal et l’aspect ordinal du nombre, ces deux aspects étant fortement liés et « une des clés de la représentation du nombre et du calcul, c’est la capacité de passer d’une vision cardinale à une vision ordinale des nombres et réciproquement. C’est notamment cette souplesse mentale qui fait l’agilité calculatoire »[2]
Activité de remédiation pour les élèves ayant besoin d’un peu plus d’entrainement
De quoi a-t-on besoin ?
Par élève, six dés, le référent-bracelet, un gobelet et d’une assiette en plastique.
Comment s’y prendre ?
Le jeu se joue par groupe de deux ou trois élèves.
Le premier enfant lance ses 6 dés dans son assiette. Il cherche le 1. S’il le trouve, il le met sur sa bandelette référent et cherche ensuite le 2…le 3… S’il n’y est pas, il reprend les dés qui restent et c’est au tour de l’enfant suivant de jouer. Le premier enfant qui a aligné ses 6 dés a gagné.

Lors des parties suivantes, on retourne la bandelette-référent et on demande à l’enfant de visualiser le dé qu’il cherche: « De quelle face as-tu besoin pour poursuivre ta suite ? La vois-tu dans ta tête avant de lancer le dé, avant de chercher dans ton assiette ? »

[1] Pour plus d’explications sur les représentations de situations mathématiques, cf. les expériences de Martine de Terwangne relatées par Anne Chevalier dans son livre : « Réussir l’entrée en mathématiques » éditions Couleur livres ASBL – 2020 (p 182)
[2] Anne Chevalier : « Réussir l’entrée en mathématiques »
