L’utilisation d’un cadran solaire – Solutions

Retour au texte introductif   De la course du Soleil aux cadrans solaires



Activités pour chercher

1. Dans une ville située à 15° (un vingt-quatrième de 360°) à l’est de Greenwich, le Soleil est ”en avance” d’une heure. Moscou se situant 37°30’ ( de 360°) à l’est de Greenwich, le Soleil passe à son méridien 2h30 avant de passer à celui de Greenwich. Alors qu’il est midi solaire à Moscou, il n’est encore que 9h30 (solaire) à Greenwich.

2. À Bruxelles, qui se situe à 4°21′ Est, le Soleil est “en avance” de h, soit de 0h17’24”. Il faut donc enlever 17’24”  à l’heure lue sur un cadran solaire à Bruxelles pour obtenir celle lue sur un cadran solaire à Greenwich.

3. a. Le trajet de la Terre autour du Soleil et les deux premières lois de Kepler.

Selon la deuxième loi de Kepler, le rayon-vecteur reliant une planète au soleil balaie des aires égales en des temps égaux. La Terre a donc une vitesse angulaire plus grande lorsqu’elle est proche du Soleil.

Quand la Terre se déplace avec une vitesse supérieure à sa moyenne, cela allonge la durée du jour solaire car, avant qu’un même méridien se retrouve face au soleil, la Terre devra effectuer une rotation d’une amplitude plus grande. Quand la Terre se déplace avec une vitesse inférieure à sa moyenne, cela raccourcit la durée du jour solaire.

Sur le schéma (exagéré) ci-dessous, le 4 janvier, le Soleil passe à un méridien (flèche rouge). Pour se retrouver dans la même situation par rapport au Soleil (flèche noire), il devra compléter le tour (rouge) d’un angle (vert) plus grand qu’à un autre moment de l’année. Cela lui prendra plus de temps.

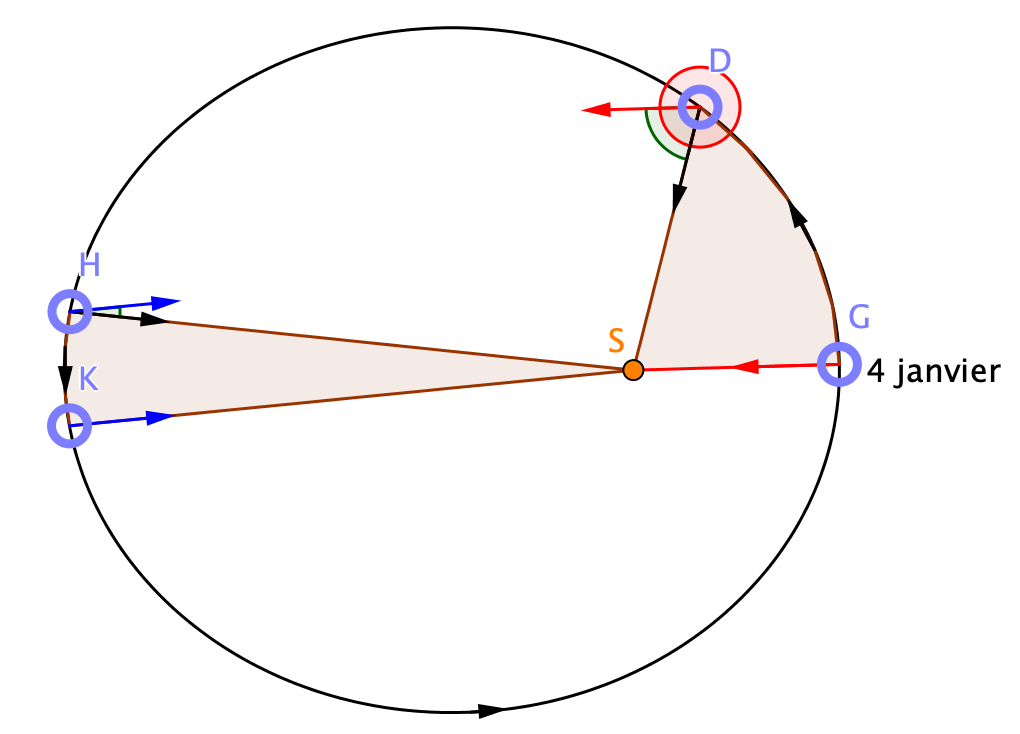
b. L’inclinaison de l’écliptique.

Si l’on néglige les conséquences du point a (car les deux foyers de l’ellipse sont assez proches), durant deux laps de temps identiques (par exemple un douzième d’année), le Soleil parcourt une même distance sur l’écliptique (un douzième de tour complet), mais cette distance ne correspond pas à un même écart entre méridiens.

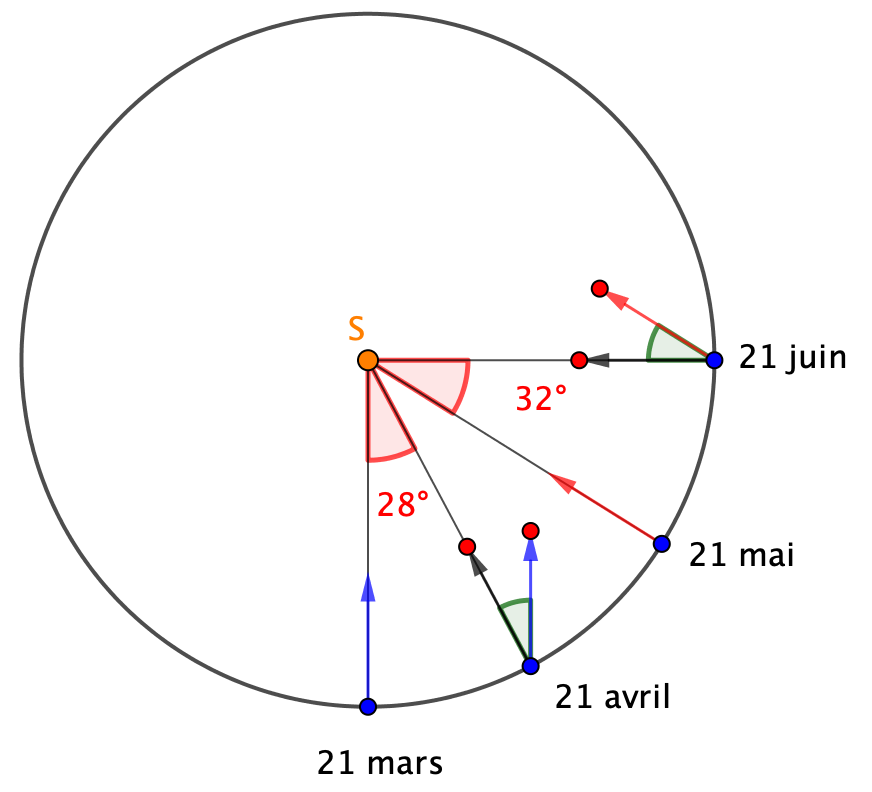
Modifiez le curseur de la figure animée ci-dessus pour placer 28° entre le méridien du Point Vernal (vers le 21 mars) et celui du Soleil un mois plus tard (angle bleu d’environ 30°). L’angle (rouge) n’est que de 28° environ, alors qu’entre ce méridien correspondant à un angle bleu de 60° (vers le 21 mai) et celui qui correspond au solstice d’été (21 juin), l’angle rouge varie d’environ 32° (ou 33°).

Aux environs du 21 mars, la durée du jour vrai est plus courte car la Terre doit tourner d’un angle plus petit qu’aux environs du 21 juin ou du 21 décembre.

Dans le document en annexe (Du_cadran_a_la_montre), on détermine les deux effets combinés avec plus de précision.

Un Soleil fictif

4. Voici le tableau complété.

Le 29 décembre, à Greenwich, il faudra ajouter 2 minutes et 26 secondes à l’heure lue sur le cadran solaire pour obtenir l’heure de la montre. En février, cette différence peut atteindre 14 minutes. Début novembre, à Greenwich, il faudra retirer une quinzaine de minutes à l’heure lue sur le cadran solaire pour obtenir l’heure de la montre.

Comment calculer l’heure de nos montres à partir de l’heure lue sur le cadran solaire ?

5. Lorsqu’il est 12.00 à Greenwich, il est 13.00 à nos montres (car nous ne sommes pas dans le même fuseau horaire). Voici la procédure pour connaître l’heure de nos montres à l’aide du cadran solaire le 1er février pour une ville située à 50° de latitude Nord et à une longitude de 4°21’ Est.

a) Supposons que l’on lise 10 h sur le cadran. Ce que nous donne le cadran solaire est : TSV + 12h = 10h.

b) Pour obtenir le temps solaire vrai +12h à Greenwich (en tenant compte de la longitude du lieu), on enlève 17’24” : on obtient 9h42’36”.

c) L’équation du temps est de 13’30” le 1er février (on peut en lire une approximation sur le graphique ou chercher cette donnée sur le Net). On en déduit le temps solaire moyen TSM + 12 h, à Greenwich = Temps universel = TU = 9h42’36” + 13’30” = 9h56’06’’.

d) Pour obtenir le temps légal en Belgique, on ajoute une heure (en hiver) : il est 10h56’06”.

e) Si, le 1er février, on lit 10h sur le cadran à Bruxelles, c’est qu’à notre montre, il est 10h56’06”. Ce jour-là, il faudra donc ajouter approximativement 56 minutes à l’heure (approximative) lue pour obtenir l’heure à nos montres.

Activités pour appliquer

1. Le 1^er février, le Soleil passera à 12h56’06’’ au méridien.

2. Pour qu’un cadran solaire indique minuit, il faut que le Soleil l’éclaire à ce moment. Cela ne peut arriver qu’au-delà des cercles polaires.

Retour au texte introductif   De la course du Soleil aux cadrans solaires