_
De quoi s’agit-il ?
Il s’agit de décrire la construction d’un assemblage de cubes par dessins successifs représentant chacun une étape de la construction pour permettre la construction d’un assemblage identique.
Enjeux
– Dessiner pour être compris
– Traduire une perception visuelle en représentation graphique et inversement
– Choisir un code de représentation de l’assemblage et s’y tenir pour permettre la compréhension des dessins et des positions des cubes les uns par rapport aux autres
– Décomposer l’assemblage complet en séquences pour le faire reconstruire
– Comprendre le cheminement de quelqu’un d’autre
– Socles 3.2.2 : Associer un solide à sa représentation dans le plan et réciproquement
– Socles 3.2.2 : Représenter un parallélépipède en perspective cavalière
– Socles 3.2.3 : Dans un contexte de reproduction de dessins, relever la présence de régularités
– Socles 3.2.3 : Décrire les différentes étapes d’une construction en s’appuyant sur des propriétés de figures, de transformations
De quoi a-t-on besoin ?
– de 10 à 20 cubes qui s’attachent pour chaque groupe d’enfants
– feuilles quadrillées (0,5 mm) ou autres et de quoi écrire
Comment s’y prendre ?
Les élèves se groupent par deux ou trois. La consigne est la suivante : « Construisez un assemblage de cubes. Dessinez ensuite les étapes de construction de cet assemblage. Ces dessins seront donnés à un autre groupe. Les mots sont interdits. Vos dessins sont réussis si l’autre groupe arrive à reconstruire un assemblage identique au vôtre ».
Les dessins sont redistribués dans d’autres groupes qui construisent un assemblage en suivant les instructions de leurs camarades.
Echos d’une classe (6e primaire)
Dessins de Sevil et Ioana :
Il faut interpréter ce qui suit comme une charade : la réunion des trois premiers éléments (n°1, 2, 3) donne le tout (n°4). On ne précise pas les positions des cubes les uns par rapport aux autres. C’est une observation du dernier schéma qui permet de comprendre comment les trois premiers éléments s’assemblent.
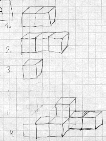
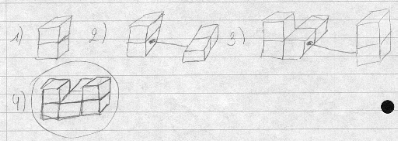
Dessins de Laetitia et Barije :
Quatre étapes sont données, la quatrième est le résultat à obtenir.
Les enfants ont relié les faces des cubes qui doivent s’accrocher, ce qui nous permet de comprendre visuellement la manière des les assembler.
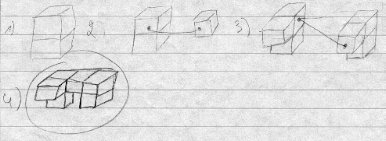
Dessins de Mahdi et Billy :
Les enfants ont dessiné trois éléments en indiquant par des flèches la manière de les accrocher. Ils n’ont pas représenté le résultat final.
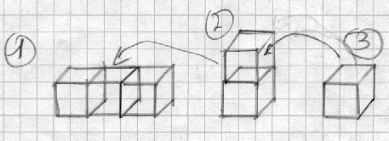
Dessins de Juliette et Karolina :
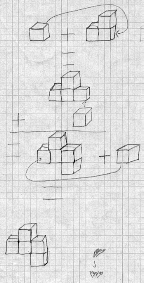
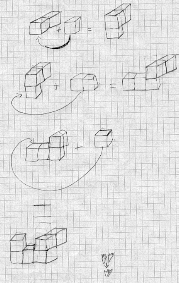
Les enfants ont utilisé la technique de la réunion, de l’assemblage en utilisant le signe de l’addition. Ils ont découpé la construction en trois séquences en utilisant des flèches pour nous indiquer la manière d’assembler les cubes.
Difficultés rencontrées :
– Comment faire pour dessiner ?
On peut construire une collection de cubes identiques en perspective parallèle. Ce matériel permet aux enfants, en superposant ces cubes en 2D, de visualiser la représentation plane de l’assemblage avant de la dessiner.
– Par où commencer mon dessin pour ne pas devoir trop gommer ?
– Que faire des lignes parasites, celles dont je n’ai plus besoin ?
Prolongements
– Varier le nombre de cubes
– Utiliser des cubes qui ne s’attachent pas, qui se déposent les uns sur les autres
– Proposer des supports papier différents : papier pointé (disponible sous format A4 en annexe), feuille blanche, …
– Complexifier les assemblages : un assemblage où certains cubes sont cachés par d’autres, par exemple
– Limiter le nombre d’étapes à dessiner
– site wisweb
Commentaires
Cette activité nécessite d’être familiarisé avec les représentations planes sur un quadrillage ou sur papier pointé (disponible en annexe). Elle fait suite aux activités des chapitres précédents.
Le fait d’interdire les mots durant cette séance provoque chez les enfants le découpage en dessins séquentiels. Cela oblige à structurer l’assemblage de plusieurs façons, à changer de points de vue pour comprendre la pensée des autres. Ne pas donner le nombre exact de cubes dans un assemblage oblige le lecteur à lire les dessins jusqu’au bout. Plus le nombre de cubes est important, plus l’activité est difficile.
Cette activité a également été menée avec un groupe d’enseignants.
Voici quelques réalisations :
Proposition 1 :
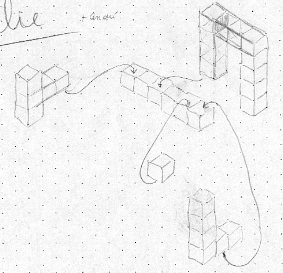
Les différents éléments de l’assemblage sont dessinés dans leur entièreté. Les flèches permettent de visualiser l’accrochage. Il n’y a pas de représentation globale de l’assemblage.
Proposition 2 :
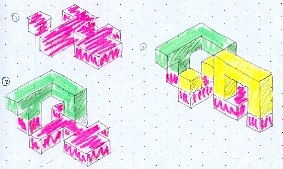
Il y a trois étapes de construction. Une couleur est ajoutée à chaque étape pour mieux visualiser les nouveaux éléments. Ce système permet de ne pas avoir d’ambiguïté de cubes cachés. Le dernier dessin représente l’assemblage dans son entièreté.
Proposition 3 :
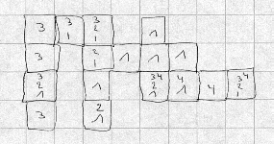
Une vue aérienne de l’assemblage est représentée. Les nombres indiqués dans les carrés représentent les étages. Par exemple, un « 3 » signifie qu’il y a un cube au troisième étage. Un « 1, 2, 3 » signifie qu’il y a un cube au premier étage, un cube au deuxième étage et un cube au troisième étage.
Ce mode de représentation est très rapide et très accessible. Il permet au dessinateur de ne pas devoir maîtriser le dessin en perspective cavalière pour s’en sortir. Il permet aussi de régler les problèmes de surplomb et de cubes cachés. Enfin, il n’exige pas de décomposer l’assemblage…

