De quoi s’agit-il ?
Dessiner un assemblage de six cubes sans contrainte quant au type de représentation. Se référer au dessin pour reconstruire le même assemblage.
Enjeux
– Sélectionner ce qui est utile dans ce qui est vu pour permettre une reconstruction à l’identique ;
– Se donner implicitement un code graphique permettant de représenter un assemblage par le dessin, et se tenir à ce code ;
– Repérer les ambiguïtés dans une représentation plane et effectuer des choix pour éliminer (limiter) ces ambiguïtés.
De quoi a-t-on besoin ?
De 6 cubes par groupe de deux élèves.
Certains matériels permettent un travail plus précis, comme les cubes de type « Structuro » , dont les faces opposées sont de même couleur.
On pose alors une convention quant à la manière de les poser sur la table, par exemple :
- jaune : faces supérieure et inférieure
- rouge : faces de devant et derrière
- bleu : faces latérales.

Comment s’y prendre ?
- Par équipes de deux élèves, faire réaliser un assemblage de 6 cubes qui touchent chacun au moins un autre cube par une face complète. Essayer de réaliser des assemblages difficiles à imiter.
Les assemblages sont tenus cachés des autres enfants (ou équipes) et serviront de témoin lors de la troisième étape du travail. - Faire dessiner, sur papier blanc sans trame, la construction de telle façon qu’on soit certain qu’une autre équipe pourra la refaire. Le papier sans trame est important afin de ne pas induire un type de représentation, de laisser le champ le plus ouvert possible à ce stade.
- Au fur et à mesure que les dessins sont prêts, les faire circuler entre les équipes qui s’en servent pour construire les assemblages représentés. À ce stade, des ambiguïtés peuvent se manifester : dans quelle position se trouve tel cube ? Où placer un cube que l’on ne voit pas sur le dessin ?
- Proposer aux enfants de repérer, dans les dessins des autres, ce qui ressemble à leur dessin, et ce qui fonctionne bien dans les dessins qui utilisent un autre code de représentation que le leur.
- En fin de séance, exposer tous les dessins, et tenter de les regrouper par familles, en regardant comment les enfants s’y sont pris pour réaliser le dessin.
- Terminer en expliquant qu’on va s’entraîner lors d’étapes ultérieures du travail en utilisant chacun des codes utilisés .
À ce stade, on veillera à éviter tout jugement sur ce qui est « correct » ou pas. Au contraire, on veillera à relever ce qui « fonctionne » dans chaque dessin, à faire exprimer par les enfants ce qu’ils ont tenté de faire, dans quelle famille ils classent eux-mêmes leur dessins : « J’ai essayé de faire comme celui-là ». Il est important que chaque enfant se sente renforcé dans ses compétences débutantes !
Échos d’une classe
(4e primaire)
Lors de l’étape 5, trois familles ont été constituées :
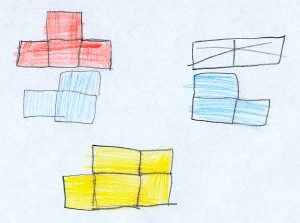
- Première famille
« On dessine de devant, et on montre un peu les autres côtés [traces de couleurs].»
 |
| Figure 1 |
- Deuxième famille
« On essaye de dessiner tous les côtés [faces] qu’on peut voir en même temps. Mais on ne peut jamais voir tous les côtés à la fois ! »
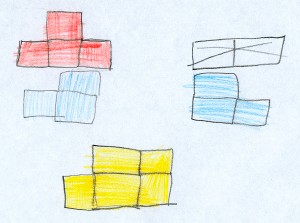 |
| Figure 2 |
- Troisième famille
« On dessine ce qu’on voit par chaque couleur séparément. »
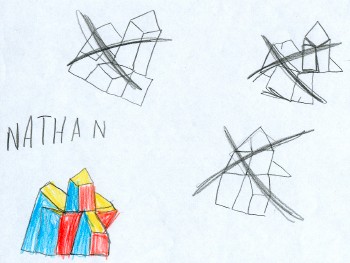 |
| Figure 3 |
Des expressions comme « 2D », « vue du dessus » ont été utilisées spontanément par les enfants. Dans les familles correspondantes, on peut préciser le vocabulaire en utilisant les mots « perspective », « vue de face, de devant, de dessus, de côté » qui reviendront dans les activités ultérieures.
Prolongements
- Relancer la recherche d’autres manières de représenter les assemblages, qui n’auraient pas encore été trouvées.
- Cette activité peut être reprise plusieurs fois en proposant d’affiner les dessins.
- Varier le nombre de cubes pour moduler la difficulté.
Vers où cela va-t-il ?
On reconnaît, dans les productions des enfants, des représentations qui annoncent la représentation frontale (fig. 1), les 3 vues orthogonales (de face, de haut et de profil) (fig. 2), et la représentation en perspective (fig. 3).
Le fait de limiter strictement le nombre de cubes à 6 dans cette activité permet de lever de nombreuses ambiguïtés : si on voit les 6 cubes dans le dessin, on est certain qu’aucun n’est caché par un autre.