L’auteur d’un graphique veut souvent faire passer un message. Le lecteur ne doit pas être dupe. Il s’agit d’être à la fois critique et perspicace pour déjouer les pièges. Dans la suite, au fur et à mesure que nous approcherons différents types de graphiques, nous relèverons quelques précautions à prendre pour être un lecteur citoyen avisé.
On fait des graphiques pour de multiples raisons comme, par exemple :
- donner une synthèse d’un ensemble d’informations et/ou une vue globale d’une réalité ;
- permettre l’interprétation rapide d’une analyse, d’une étude et/ou un contrôle de résultats ;
- faciliter la comparaison de situations à la fois proches et distinctes ;
- montrer l’évolution de certains phénomènes.
Quand on passe d’un contexte, d’un tableau de données ou d’une formule à une représentation graphique, on devrait soigner :
- la lisibilité car un graphique doit être plus directement et rapidement lisible que les données chiffrées.
- la fidélité car un graphique ne peut ni trahir les données, ni tronquer la réalité. Certains graphiques sont corrects d’un point de vue formel mais trompeurs, de façon intentionnelle ou non, parce qu’ils donnent une impression visuelle qui déforme la réalité.
- l’auto suffisance car un graphique doit pouvoir être compris indépendamment du tableau de don- nées ; le titre, le libellé des axes, les échelles et les sources sont des éléments importants constitutifs du graphique.
1 Des bâtons et des points
1.1 En bâtonnets
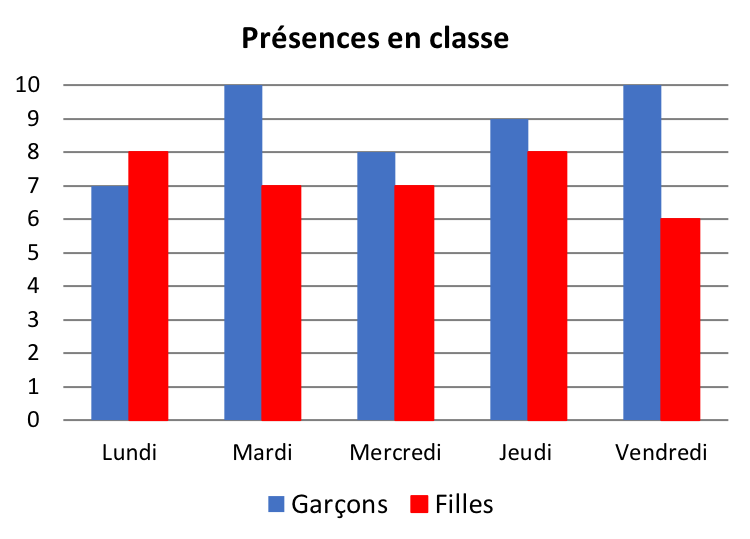
Tous les matins dans une classe de maternelle, quand un garçon entre en classe, il ajoute une brique bleue à la pile des briques bleues (figure 1). Et chaque fille fait de même avec une rouge. Au terme de la semaine, on représente la situation par un graphique en bâtons ou en bâtonnets[1]Dans certains pays comme le Québec, on parle également de graphique à bandes. et on visualise les présences en classe au cours de la semaine (figure 2).

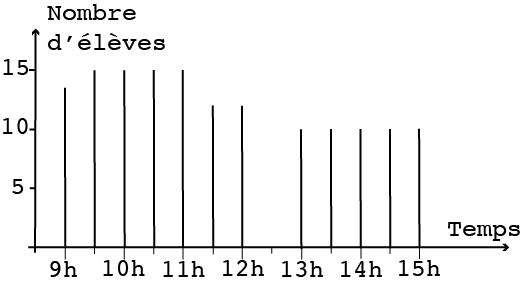
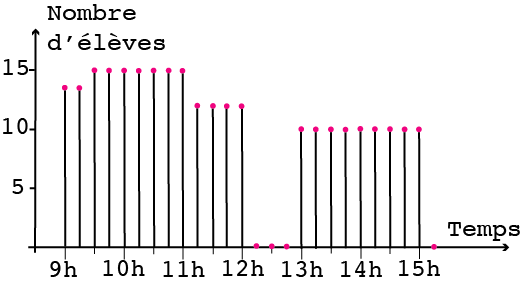
Supposons qu’on relève le nombre d’élèves présents sans distinguer les filles des garçons, non seulement pour la journée, mais toutes les demi-heures. Lundi à 9h, 13 élèves sont dans la classe. A 9h30, deux élèves arrivent encore. Juste après 11h, 3 élèves font une petite chute sur le module de jeu et sont transférés à l’infirmerie de l’école. Finalement, rien de grave pour eux, mais ils rentrent à la maison. A midi, c’est la récréation. A 13h, deux petits ne sont pas revenus. Le relevé demi-heure par demi-heure conduit au graphique de la figure 3. Les bâtonnets ont subi une petite cure d’amaigrissement mais ce sont toujours des bâtonnets…
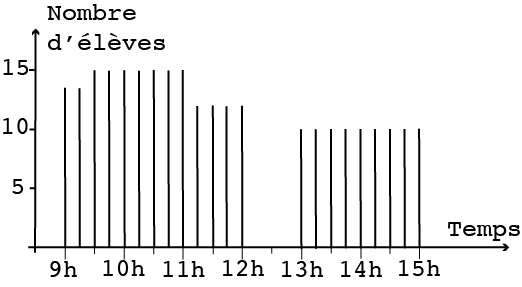
On peut aussi faire le relevé tous les quarts d’heures et aboutir à la figure 4.
1.2 À points
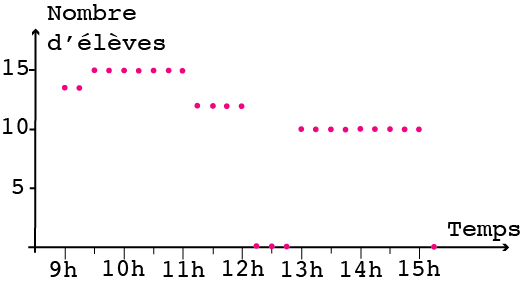
Il n’est pas indispensable de considérer le bâtonnet dans son entièreté alors que c’est sa hauteur qui est déterminante (figure 5). On peut donc se contenter de représenter le sommet du bâtonnet comme à la figure 6.
1.3 En segments ou en courbes
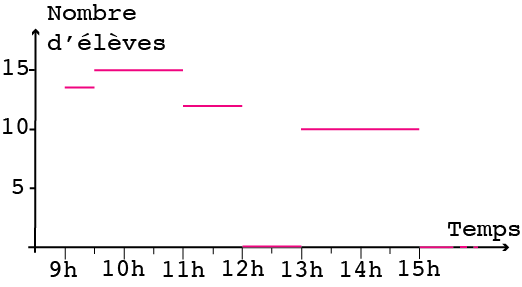
Avec ce système de points pour remplacer les bâtonnets, si on fait le relevé des présences toutes les minutes, toutes les secondes, tous les instants… On a un graphique comme celui de la figure 7. Et si on veut être précis sur ce qui se passe en certaines valeurs comme à 9h30, 11h, 12h, 13h, 15h, on marque par un point plein l’effectif (le nombre d’élèves) correspondant et par un point vide l’effectif qui ne correspond pas à ce moment. S’il y avait 14 présents en classe à 9h29 et qu’un élève est arrivé à 9h30 précises: à 9h30, on a donc un point plein sur le nombre 15 et un point vide sur le nombre 14. Le graphique de la figure 8 est un graphique cartésien. L’axe du temps est l’axe des abscisses. L’axe du nombre de présents ou de l’effectif est l’axe des ordonnées.
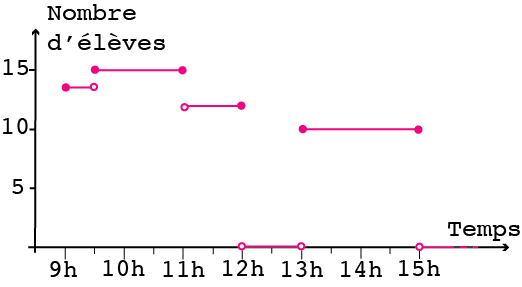
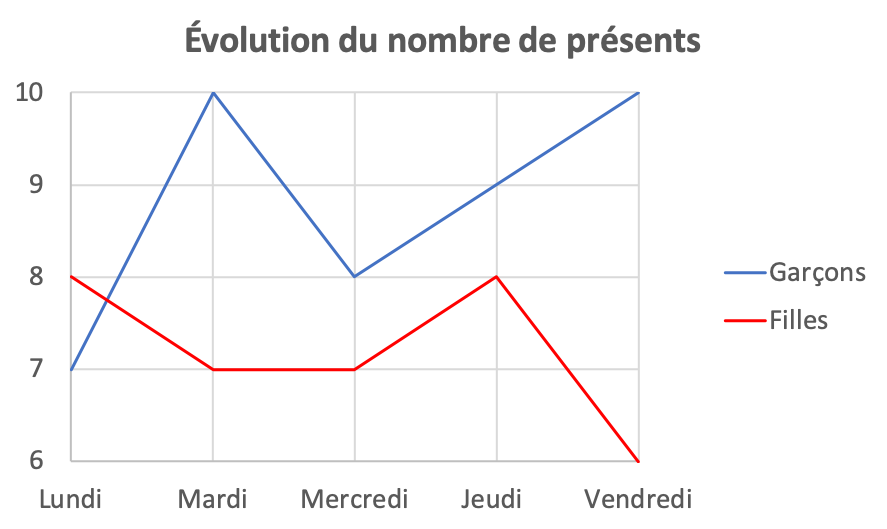
À la figure 8, on a donc relié des points de façon tout à fait naturelle. Reprenons le graphique de la figure 2, imaginons à nouveau que les sommets des bâtonnets suffisent pour caractériser le nombre de filles et de garçons présents en classe. Peut-on relier les sommets comme on l’a fait à la figure 9 ?
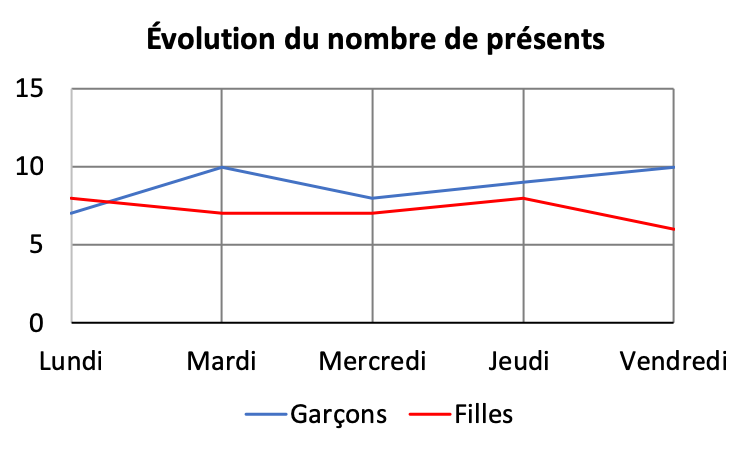
Lundi, par exemple, 8 filles sont venues en classe. Mardi, il y en avait 7. On relie les deux points par un segment. Chaque point de ce segment correspond-il à la présence de filles à un moment donné ? Non ! Le segment montre la tendance, l’évolution d’un jour à l’autre tandis que les points qui le composent n’ont pas de sens en termes d’effectifs. Les graphiques des figures 8 et 9 sont des graphiques cartésiens évolutifs car c’est le temps qui est la variable indépendante. Et dans ces deux cas, la variable dépendante est le nombre d’élèves.
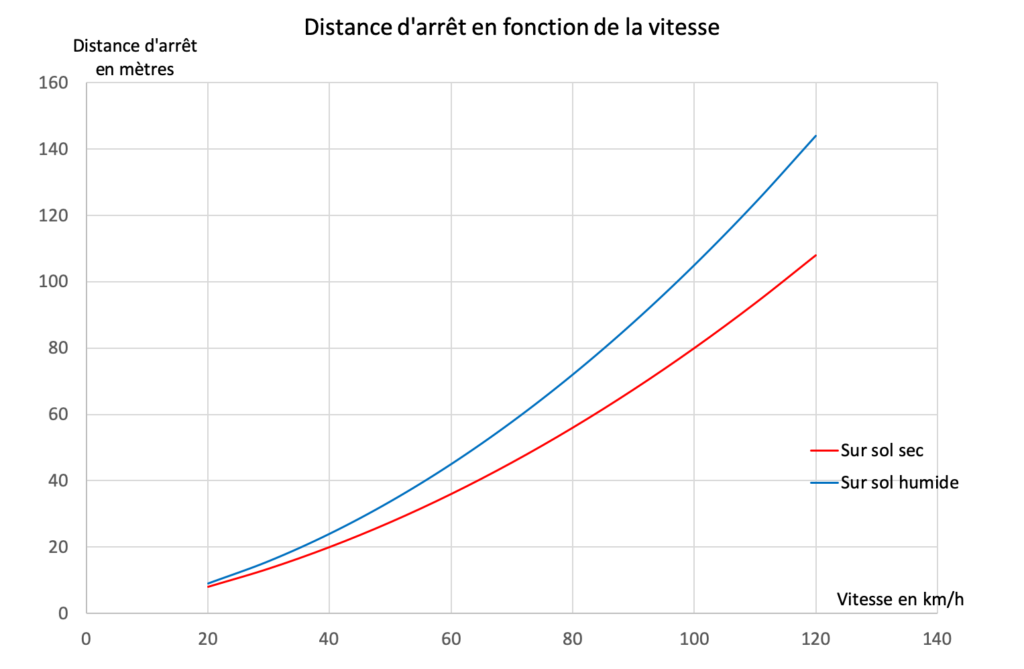
À la figure 10, on a représenté la distance d’arrêt d’un automobiliste[2]Selon « Permis de conduire-Online à l’adresse https://www.permisdeconduire-online.be/snelheidwet6.htm. Consulté le 8 décembre 2019. par temps sec et par temps humide. La variable indépendante n’est pas le temps mais la vitesse du véhicule, la variable dépendante est la distance d’arrêt. Il s’agit encore d’un graphique cartésien.
1.4 Pas de sens ou trompeur
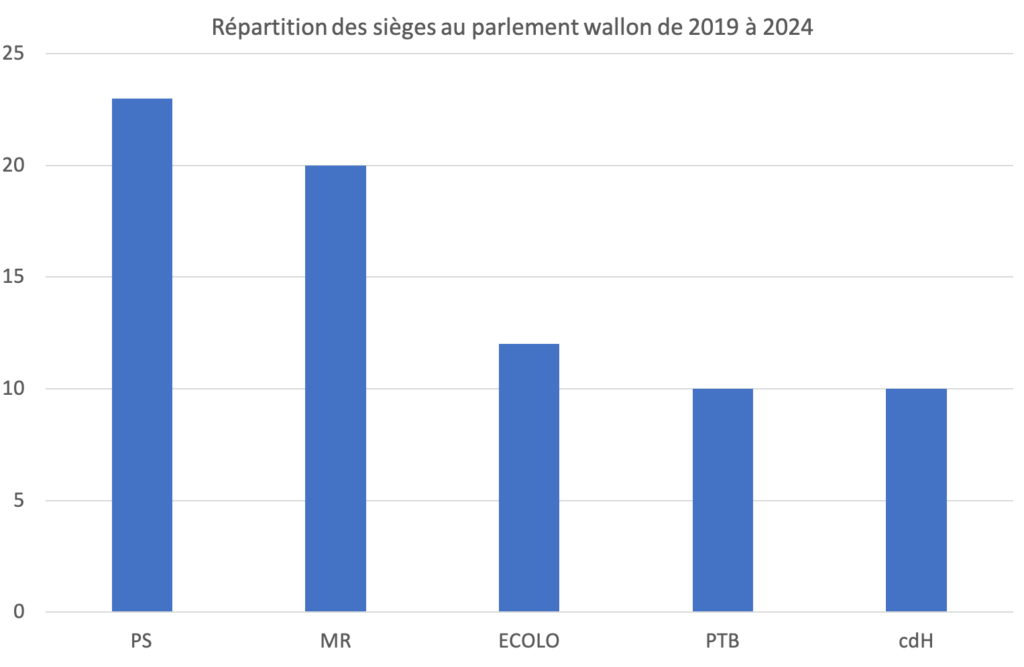
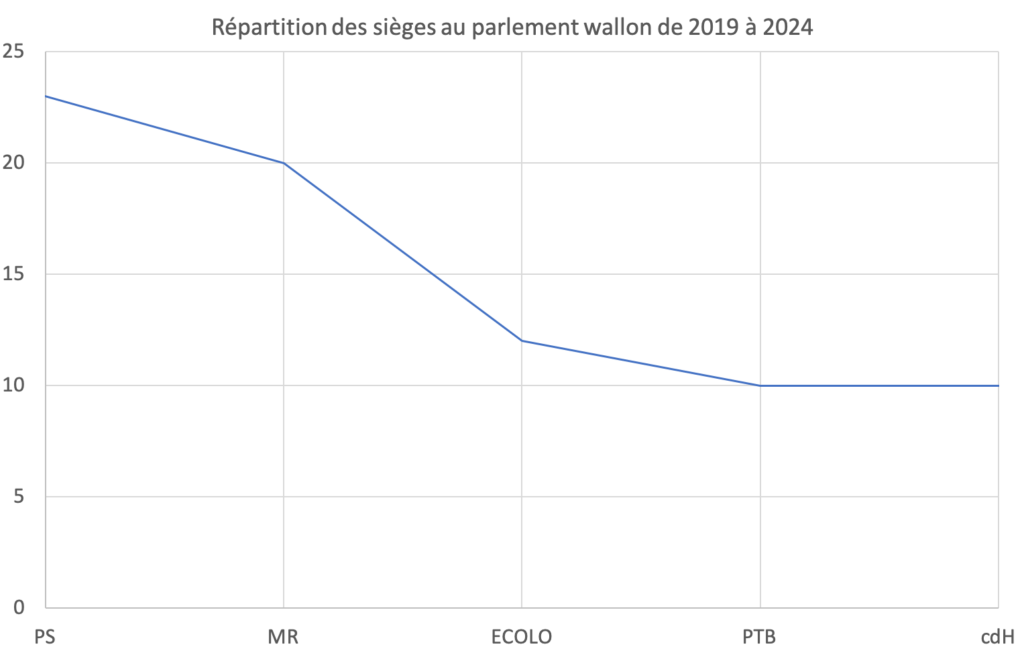
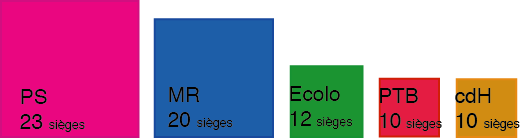
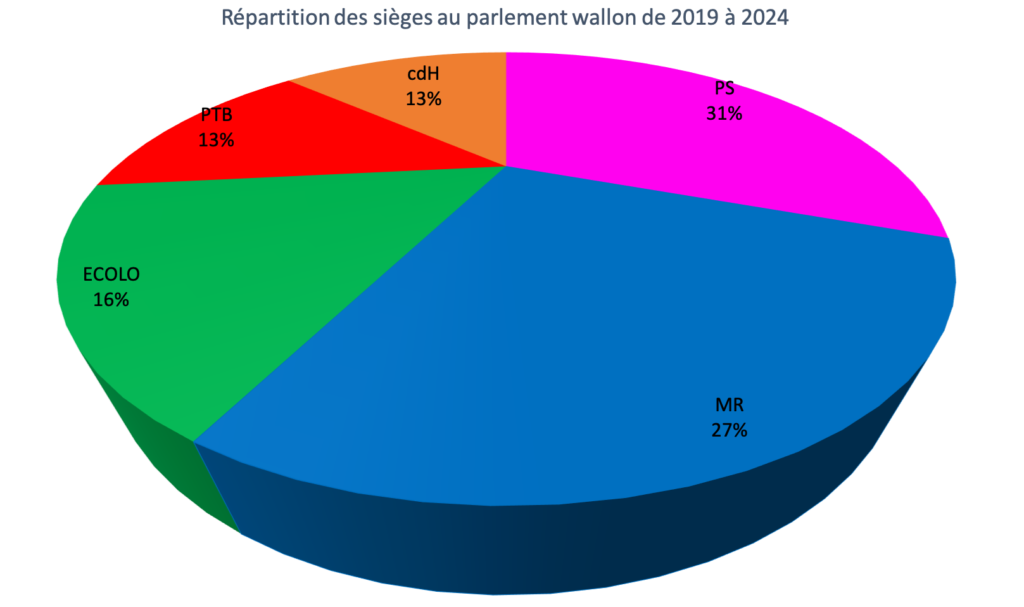
Sur certains graphiques cartésiens, on relie des points et cela prend tout son sens comme aux figures 8 et 10. Pour d’autres graphiques cartésiens, on relie des points pour montrer une évolution comme à la figure 9. Mais il y a des cas où relier des points pose problème. À la figure 11, on a représenté par un graphique en bâtonnets la répartition des sièges au parlement wallon depuis les élections de 2019. À la figure 12, on a considéré un graphique cartésien avec des points pour représenter le nombre de sièges de chaque parti. Mais quel est le sens des segments qui relient ces points ? Absolument aucun…
Le graphique de la figure 13 représente les mêmes données que celui de la figure 9. Mais l’axe des ordonnées est gradué différemment. L’origine n’est pas en 0 mais en 5 et l’étendue couverte est de 4 et non de 15. Cela fait croire à des variations de présence plus importante d’un jour à l’autre. Il s’agit d’un effet qui peut être trompeur…
2 Des aires
2.1 Circulaire
On peut représenter la répartition des sièges au parlement wallon au travers d’un graphique circulaire que certains qualifient, en termes plus culinaires et fleuris, de graphique en quartiers de tarte ou de camembert (figure 14). On considère un disque et on consacre à chaque parti un secteur angulaire dont l’angle est proportionnel au nombre de sièges sachant que 100 % des sièges correspondent à 360°. Sur les 75 sièges du parlement wallon, le PS par exemple est majoritaire et en dispose de 23. Il lui correspond donc un secteur angulaire d’amplitude ![]() .
.
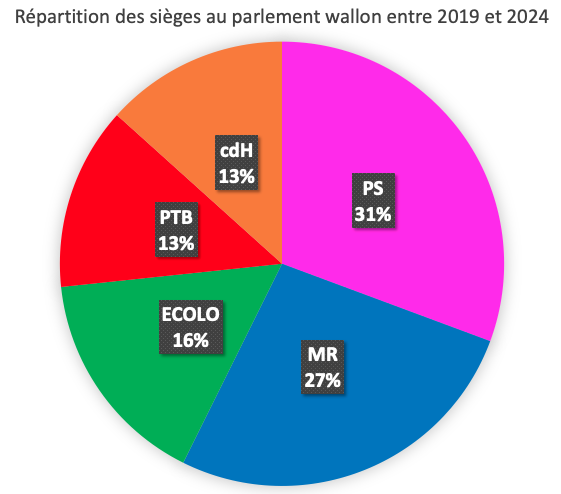
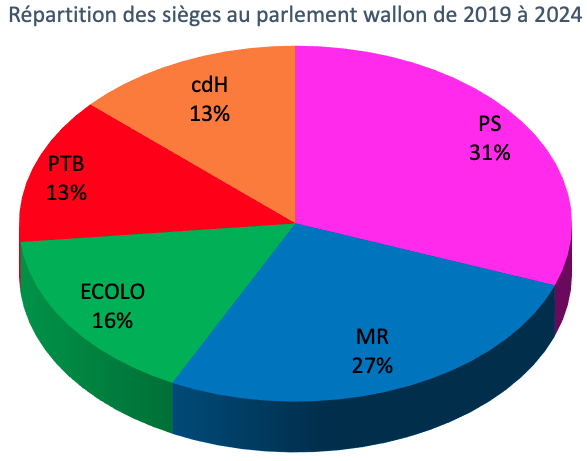
Figure 15
En regardant un graphique comme celui de la figure 14, sommes-nous sensibles aux amplitudes d’angle des secteurs, ou plutôt à leur aire? Dans ce cas-ci, c’est pareil puisque les aires sont proportionnelles aux amplitudes d’angle et au nombre de sièges.
Mais pour le graphique de la figure 15, construit à partir des mêmes données que celui de la figure 14, avec un effet de perspective axonométrique, ce n’est plus un disque qu’on obtient, mais une ellipse. D’intention esthétique, la démarche n’est cependant pas neutre: cela a visiblement pour conséquence de donner plus d’importance au MR que ce que lui donne le graphique de la figure 14. Mais n’est-ce qu’une impression ? Quelle transformation permet le passage de l’un à l’autre ? Avec quels effets ?
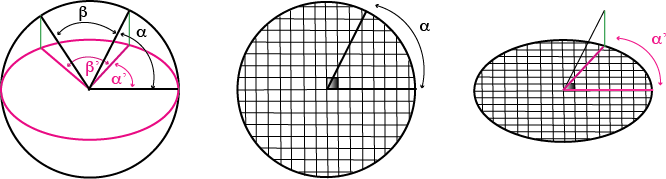
Le disque est transformé en ellipse par affinité.[3]Voir l’annexe A pour en savoir plus sur l’affinité. On constate que les amplitudes d’angles ne sont pas conservées (figure 16, à gauche), certaines subissent une augmentation et d’autres une diminution. Par contre, comme il s’agit d’une affinité, les aires des secteurs angulaires du cercle et de l’ellipse sont proportionnelles entre elles dans un rapport qui correspond au rapport d’affinité. On peut s’en convaincre intuitivement en quadrillant finement le disque avec une famille de lignes parallèles à l’axe de l’affinité et l’autre de lignes perpendiculaires (figure 16, au centre). Les carrés du quadrillage initial sont tous transformés en rectangles isométriques dont une dimension n’a pas changé tandis que l’autre a subi l’affinité (figure 16, à droite). En passant du disque à l’ellipse, les rapports d’aires des secteurs angulaires n’ont donc pas changés.
Par ailleurs, ce n’est pas vraiment un disque mais un cylindre qu’on a représenté en perspective qui apparaît à la figure 14. Et si on prend en compte l’épaisseur du cylindre, on constate que la différence de traitement est très nette entre les secteurs situés en arrière et ceux situés en avant : pour ceux-ci (MR et ECOLO) l’impact visuel est renforcé par la tranche visible du cylindre.
2.2 Rectangle
Le graphique de la figure 17 illustre également la répartition des sièges au parlement wallon depuis les élections de 2019. La figure de référence n’est plus un disque mais un rectangle et l’aire attribuée à chacun des partis est toujours proportionnelle au nombre de sièges dont il dispose dans ce parlement.

2.3 Entre deux courbes
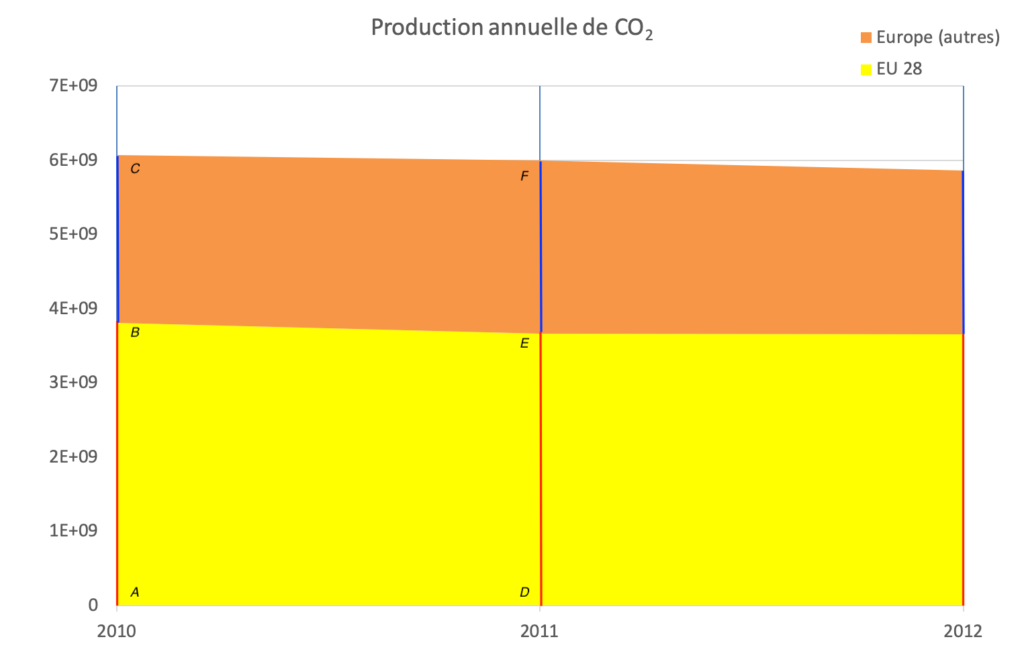
La figure 18 nous renseigne sur la production totale annuelle de ![]() par région[4]Source des données : Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019., pour un année donnée. Chaque courbe séparant deux aires de couleurs différentes correspond à la production cumulée des régions représentées sous cette courbe. La courbe qui délimite les aires « jaune » et « orange », par exemple, correspond à la production totale annuelle de
par région[4]Source des données : Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019., pour un année donnée. Chaque courbe séparant deux aires de couleurs différentes correspond à la production cumulée des régions représentées sous cette courbe. La courbe qui délimite les aires « jaune » et « orange », par exemple, correspond à la production totale annuelle de ![]() de l’Europe des 28. La courbe qui délimite les aires « orange » et « mauve » correspond à la production totale annuelle cumulée de
de l’Europe des 28. La courbe qui délimite les aires « orange » et « mauve » correspond à la production totale annuelle cumulée de ![]() de l’Europe des 28 et des autres pays d’Europe. Et ainsi de suite…
de l’Europe des 28 et des autres pays d’Europe. Et ainsi de suite…
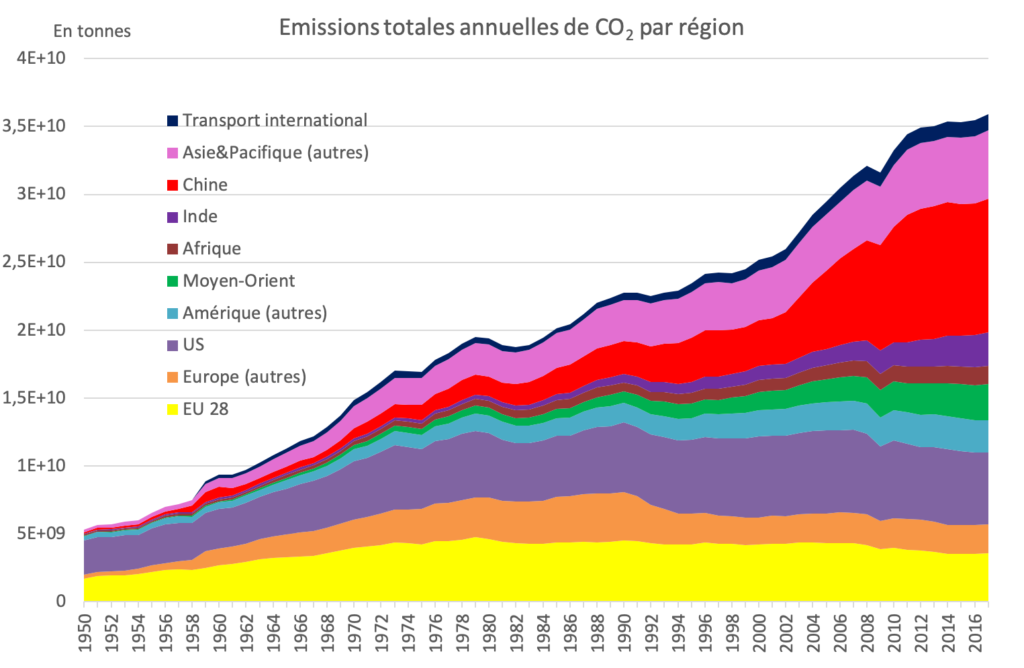
Mais à quoi correspond l’aire en dessous de la première courbe ou entre deux courbes successives ? Comme nous le montrons à l’annexe B, on peut associer chacune de ces aires aux émissions totales de ![]() de l’entité géographique associée, entre 1950 et 2007.
de l’entité géographique associée, entre 1950 et 2007.
2.4 Pas de sens ou trompeur
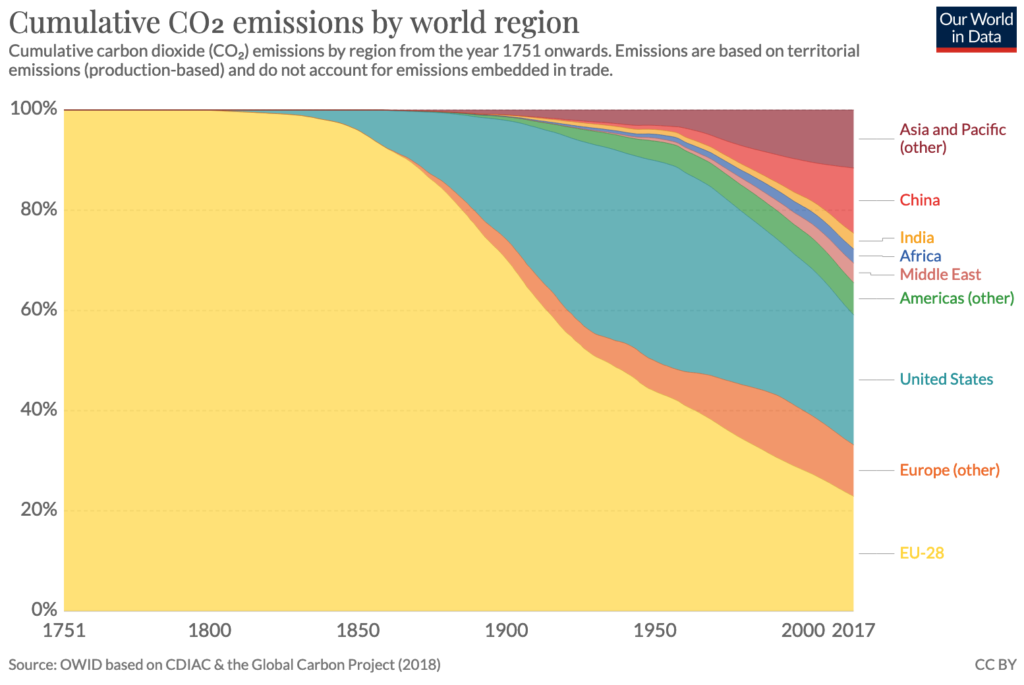
Le graphique[5]Extrait du site Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019. de la figure 19 reprend pour un certain nombre de régions du monde et pour chaque année la part de la production cumulée de ![]() depuis 1751. L’impact de l’Europe des 28 semble énorme au vu de l’aire « jaune ». Mais c’est trompeur car cette aire n’a pas de sens mathématique. En ordonnée, on a ramené pour chaque année, les émissions cumulées jusqu’à cette année et pour la planète entière, à 100 %. En 1750, ces 100 % d’émissions cumulées de la planète correspondent à 9.35 millions de tonnes; tandis qu’en 2017, ils correspondent à 1.58 mille milliards de tonnes. Soit 150 000 fois plus… Un graphique en bâtonnets eut été plus judicieux dans ce cas de figure.
depuis 1751. L’impact de l’Europe des 28 semble énorme au vu de l’aire « jaune ». Mais c’est trompeur car cette aire n’a pas de sens mathématique. En ordonnée, on a ramené pour chaque année, les émissions cumulées jusqu’à cette année et pour la planète entière, à 100 %. En 1750, ces 100 % d’émissions cumulées de la planète correspondent à 9.35 millions de tonnes; tandis qu’en 2017, ils correspondent à 1.58 mille milliards de tonnes. Soit 150 000 fois plus… Un graphique en bâtonnets eut été plus judicieux dans ce cas de figure.
Le graphique de la figure 20 donne la répartition des sièges du parlement wallon depuis les élections de 2019. Chaque parti est représenté par un carré dont la longueur du côté est proportionnelle au nombre de sièges mais c’est l’aire qui frappe avant tout le regard. Le graphique est trompeur. Alors que le MR est deux fois mieux représenté que le cdH, on peut croire que le rapport est de quatre….
2.5 Histogramme
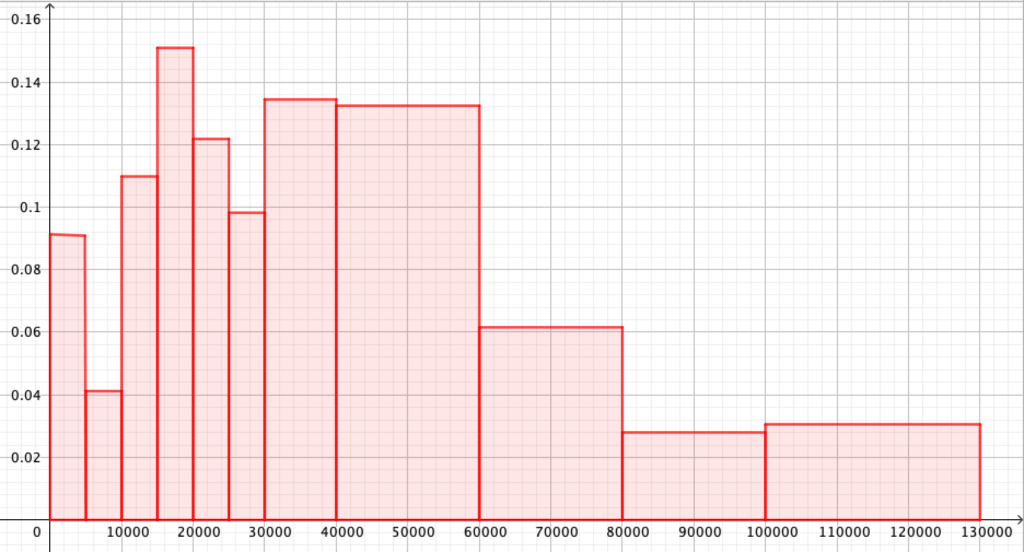
Si on étudie une variable comme les revenus nets imposables, sur une population comme les ménages belges, on a plus de six millions de données en 2017. Impossible de traiter toutes ces données individuellement et d’illustrer la situation par un graphique qui compterait des millions de bâtonnets. Pour plus de facilité, on regroupe donc les données par classes. Prenons des classes de largeur 5000 euros, puis 10000 euros, puis 20000 euros, sachant qu’il y a plus de petits que de grands revenus. On peut alors faire un graphique en bâtonnets[6]Source des données : Statbel à l’adresse https://statbel.fgov.be/fr/themes/menages/revenus-fiscaux/plus. Consulté le 10 novembre 2019. comme celui de la figure 21. En ordonnée, apparaissent les fréquences de chaque classe. La fréquence de la classe [5000,10000[, par exemple, est obtenue en divisant le nombre de ménages ayant un revenu annuel net imposable compris entre 5000 et 10000 (l’effectif de la classe), par le nombre total de ménages qui ont un revenu non nul[7]Car il faut savoir que les 547750 ménages qui ont un revenu net imposable nul, ne sont pas repris dans l’étude… (l’effectif total). On a ![]() . La dernière classe qui reprend les revenus de 100000 euros et plus, n’est pas fermée. Nous y avons quand même associé un bâtonnet de largeur 30000 euros.
. La dernière classe qui reprend les revenus de 100000 euros et plus, n’est pas fermée. Nous y avons quand même associé un bâtonnet de largeur 30000 euros.
Ce graphique est trompeur ! Car si le bâtonnet de la classe [40000,60000[ est presque aussi grand que celui de la classe [30000,40000[, c’est parce que la classe est deux fois plus large. Si on est sensible à l’aire, on a l’impression qu’il y autant de revenus de revenus entre 40000 et 50000 qu’entre 30000 et 40000… Alors que c’est entre 40000 et 60000 qu’il y en a presque autant qu’entre 30000 et 40000.
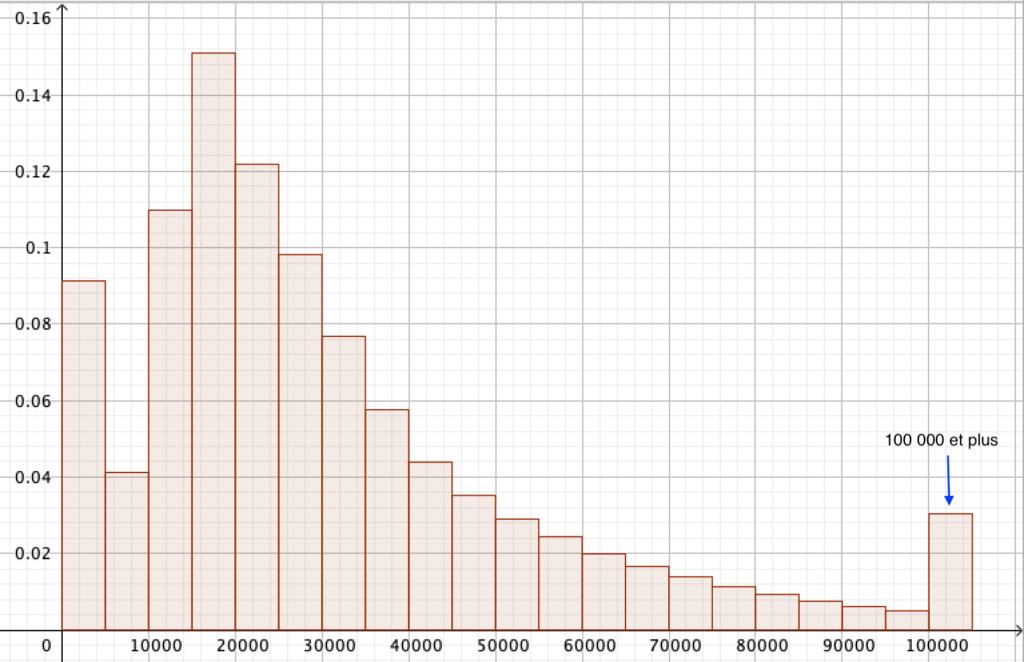
Le graphique de la figure 22 est un histogramme. Il représente les mêmes données que le graphique de la figure 21. Ce sont plus les hauteurs qui sont à prendre en compte mais les aires. Et les classes qui ne sont pas de même largeur, ne posent pas problème. Pour la dernière classe non fermée, comme on ne connaît pas le revenu maximum et qu’il est probablement très élevé (de l’ordre du million, du milliard ou plus), il faudrait considérer un rectangle très allongé et de très faible hauteur. Nous avons choisi de représenter un rectangle dont l’aire correspond bien à la fréquence de la classe même si sa forme n’est pas la bonne.
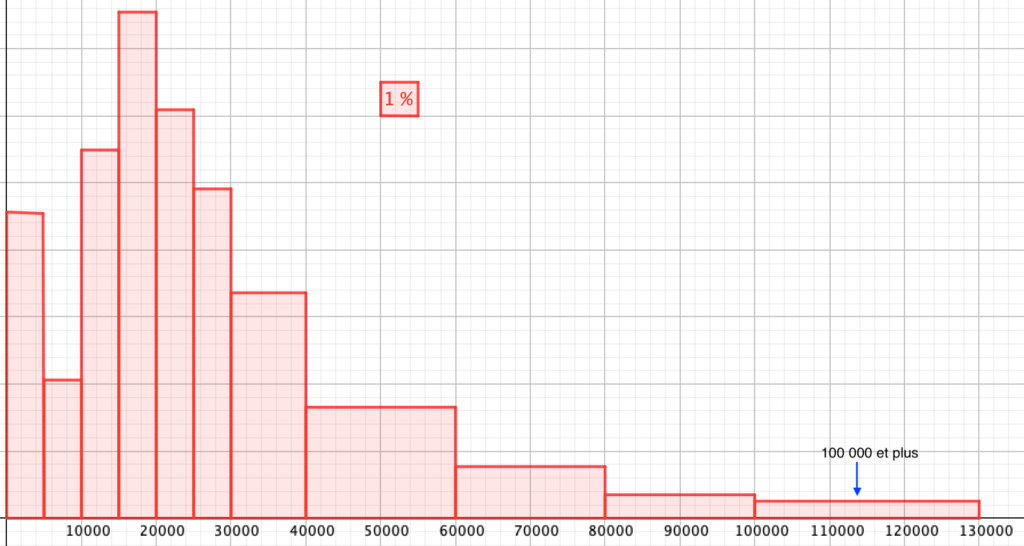
A la figure 23, on a fait un graphique en bâtonnets en considérant des classes de même largeur. L’aire des bâtonnets est donc proportionnelle à leur hauteur et ce graphique en bâtonnets peut donc être aussi considéré comme un histogramme.
3 Croissance
3.1 Relative ou absolue
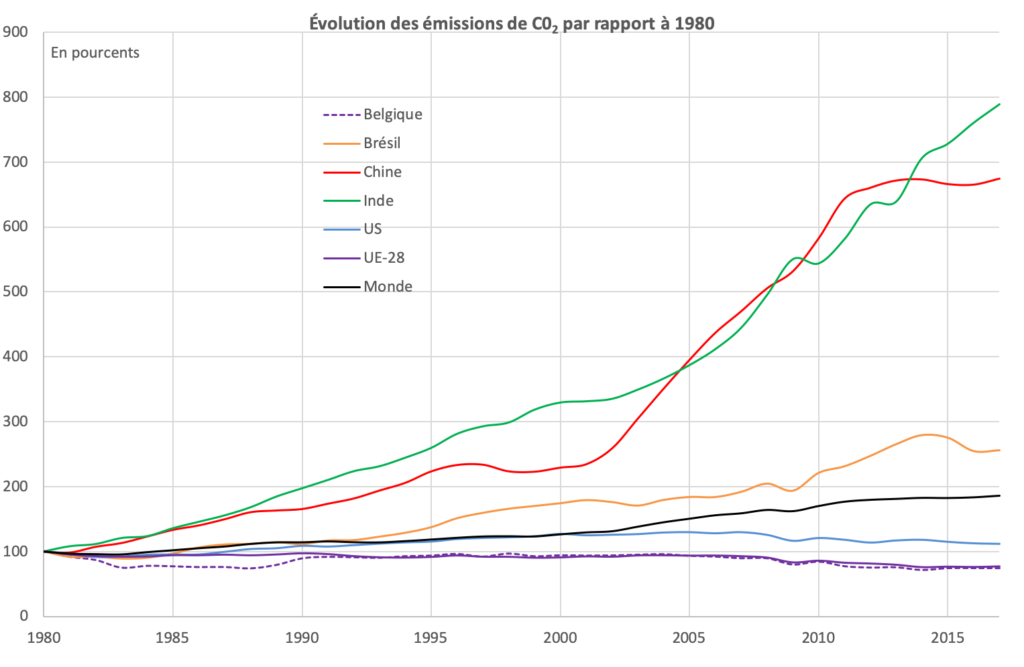
Le graphique de la figure 24 représente l’évolution des émissions de ![]() de quelques pays et régions[8]Source des données : Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019. entre 1980 et 2017. L’Inde et la Chine semblent être les plus gros émetteurs et dépassent de loin les Etats-Unis et l’Union européenne. Tous les pays sont au niveau 100 % en 1980 ! C’est parce qu’on a considéré des indices[9]La notion d’indice est développée à l’annexe A. et non des productions. Pour ce faire, il a fallu diviser, pour chaque circonscription géographique considérée et pour chaque année, la production annuelle de cette circonscription par celle de 1980. Le graphique montre que la production de
de quelques pays et régions[8]Source des données : Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019. entre 1980 et 2017. L’Inde et la Chine semblent être les plus gros émetteurs et dépassent de loin les Etats-Unis et l’Union européenne. Tous les pays sont au niveau 100 % en 1980 ! C’est parce qu’on a considéré des indices[9]La notion d’indice est développée à l’annexe A. et non des productions. Pour ce faire, il a fallu diviser, pour chaque circonscription géographique considérée et pour chaque année, la production annuelle de cette circonscription par celle de 1980. Le graphique montre que la production de ![]() a été multipliée par presque 7 pour la Chine et presque par 8 pour l’Inde entre 1980 et 2017. Mais il faudrait savoir d’où sont partis ces pays ? Quelle était l’importance de leurs émissions en 1980 et après, jusqu’en 2017 ?
a été multipliée par presque 7 pour la Chine et presque par 8 pour l’Inde entre 1980 et 2017. Mais il faudrait savoir d’où sont partis ces pays ? Quelle était l’importance de leurs émissions en 1980 et après, jusqu’en 2017 ?
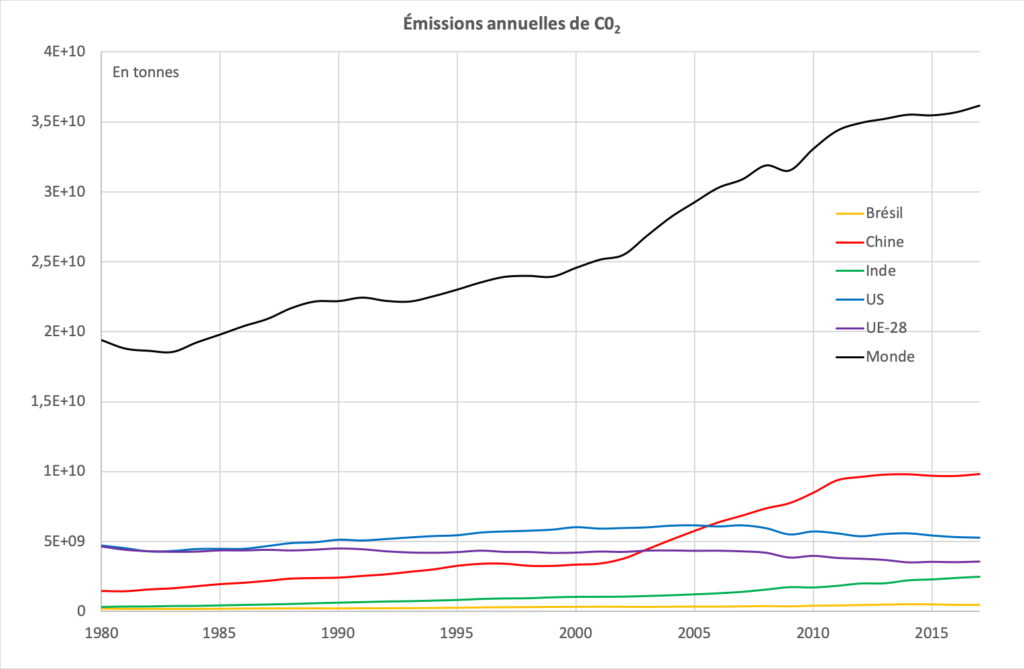
Le graphique de la figure 25 montre une réalité bien différente. Ce sont les émissions totales annuelles qui sont représentées. Ce n’est qu’à partir de 2006 que la Chine dépasse les Etats-Unis. Quelle en est la cause ? Une industrialisation galopante ? La consommation de charbon ? A moins que ce soit aussi dû à la taille de la population ?
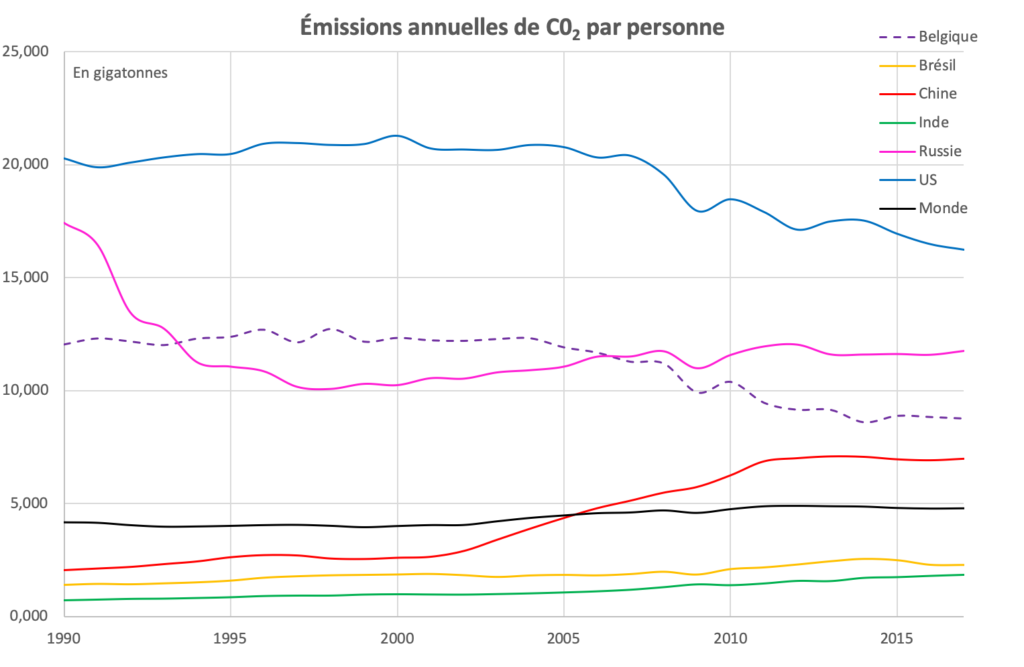
Le graphique de la figure 26 montre les émissions totales annuelles de ![]() par habitant. Une grande différence avec les deux graphiques précédents ! Ce sont les Etats-Unis qui caracolent largement en tête. L’Inde reste bien en deçà des moyennes mondiales. Cela relativise très fort le propos d’hommes politiques, américains notamment, qui enjoignent la Chine de réduire ses émissions de
par habitant. Une grande différence avec les deux graphiques précédents ! Ce sont les Etats-Unis qui caracolent largement en tête. L’Inde reste bien en deçà des moyennes mondiales. Cela relativise très fort le propos d’hommes politiques, américains notamment, qui enjoignent la Chine de réduire ses émissions de ![]() en la qualifiant de plus gros pollueur du monde.
en la qualifiant de plus gros pollueur du monde.
3.2 Modèle linéaire
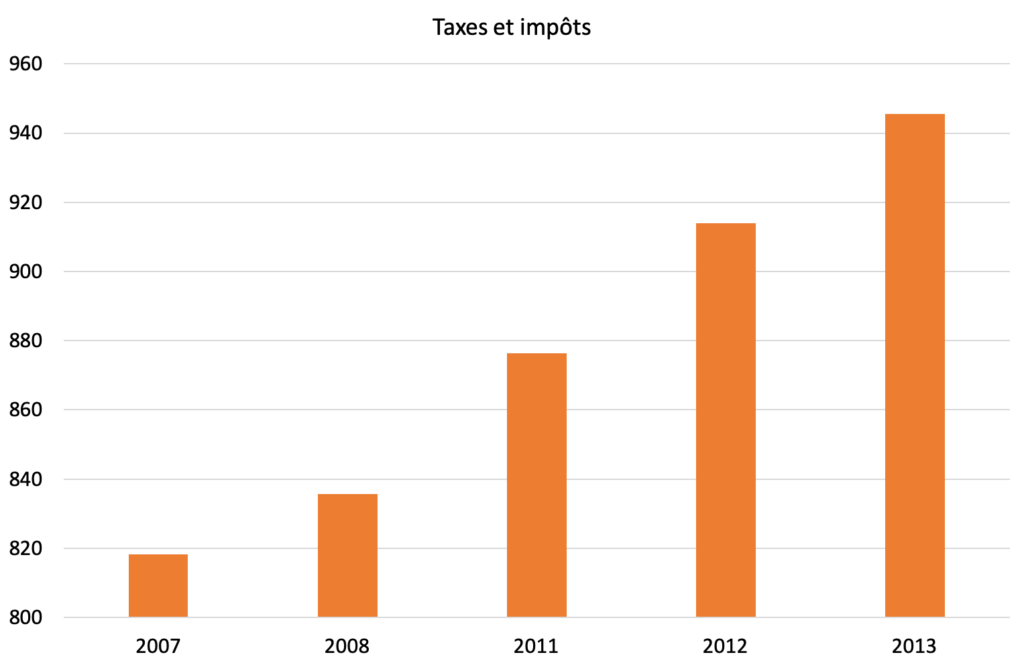
La figure 27 est extraite d’un tract électoral[10]Alexandre Pouchard, Le Monde du 15 mars 2015 à l’adresse https://www.lemonde.fr/les-decodeurs. Consulté le 11 novembre 2019 du Front national français aux élections départementales de 2015. Le FN y dénonce la situation de la France, qui subit un chômage élevé et des hausses d’impôts ces dernières années. Au vu du graphique, on a l’impression que les impôts progressent de façon constante d’année en année. Et cela paraît sérieux puisque les données sont issues de l’INSEE, l’institut national de statistique français. Le graphique de la figure 28 reprend les mêmes données au travers d’un graphique en bâtonnets.

En regardant de près, on constate un trou de deux années en abscisse. « Choix étonnant… sauf lorsqu’on constate que ces prélèvements obligatoires ont diminué en 2009 (795,8 milliards d’euros), avant de recommencer à augmenter en 2010 (825,1 milliards d’euros) et de dépasser en 2011 le niveau de 2008. La baisse de 2009 est due à la récession qui a frappé le pays cette année-là (- 2,9 \%). »[11]Alexandre Pouchard, Le Monde du 15 mars 2015. Un autre biais réside dans le choix de la graduation de l’axe en ordonnée qui ne commence pas à zéro mais à 800 milliards. En intégrant ces deux remarques, on obtient un graphique comme celui de la figure 29.
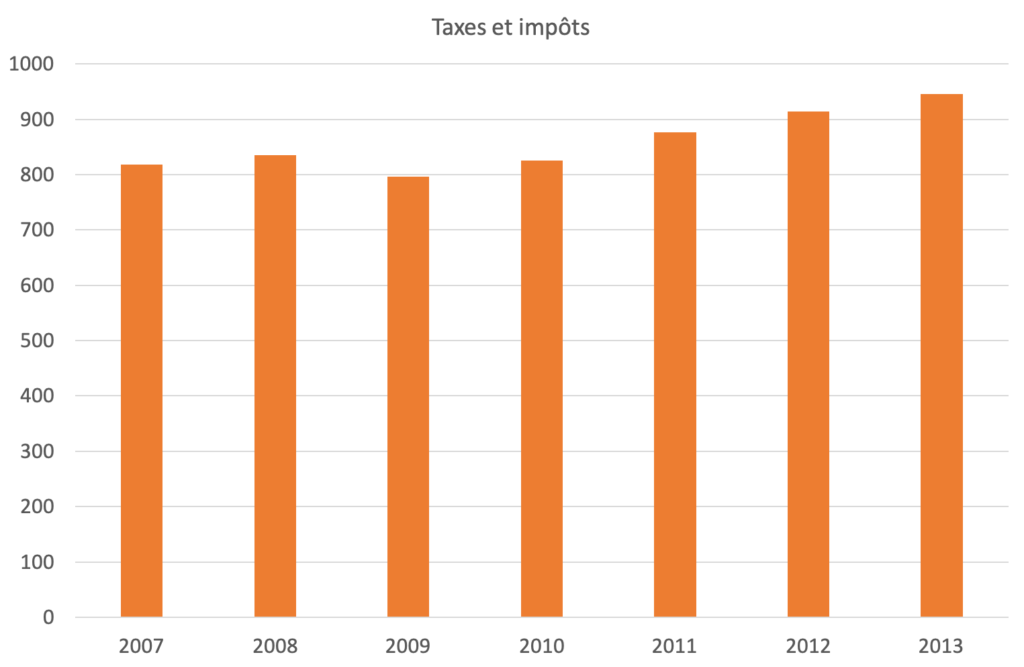
On constate une « faible » hausse de 17,4 milliards entre 2007 et 2008, soit à peu près de 2 %. Une chute importante de 39,9 milliards a lieu en 2009, soit à peu près de 4,8 %. Puis cela repart à la hausse, entre 29,3 et 51,2 milliards suivant les années. Ou de 3,7 % à 6,2 %. Mais c’est sans prendre en compte l’inflation qui a par exemple été de 1,5 % en 2010, de 2 % en 2011 et 2012, de 1% en 2013…
3.3 Modèle exponentiel
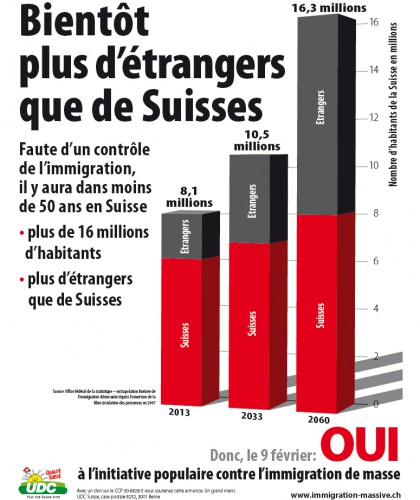
A la figure 30 apparaît une affiche de l’UDC suisse (Union Démocratique du Centre)[12]Il s’agit d’un parti d’extrême droite contrairement à ce que laisse croire son appellation. dans le cadre d’une campagne intitulée « immigration massive ».[13]Postée le 14 janvier 2014 par Lionel Baland, l’actualité des partis patriotiques en Europe à … Continue reading
En tout petit, en bas et à gauche du graphique, on peut lire : « Source : Office fédéral de la statistique, extrapolation linéaire de l’immigration démesurée depuis l’ouverture de la libre circulation de personnes en 2007 ». Que faut-il penser de cette extrapolation ? Est-elle bien linéaire ? Est-il raisonnable de prédire une tendance sur 50 ans en se basant sur des données de 2007 à 2013 ? Nous avons recherché des données fiables[14]Elles viennent de l’Office fédéral de la statistique de la Confédération suisse à l’adresse … Continue reading que nous montre la figure 31.
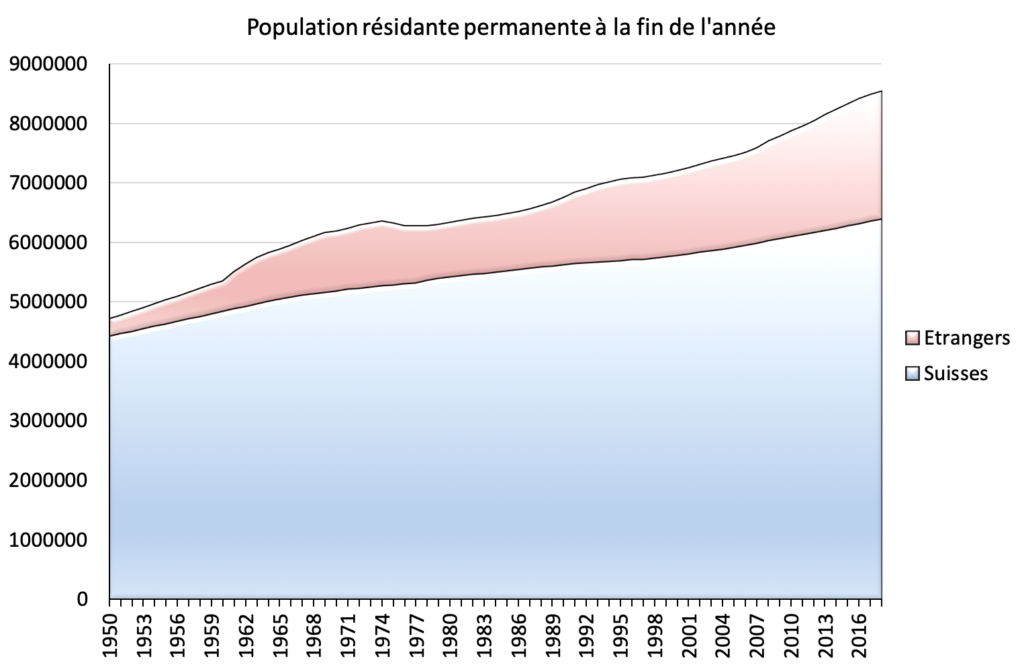
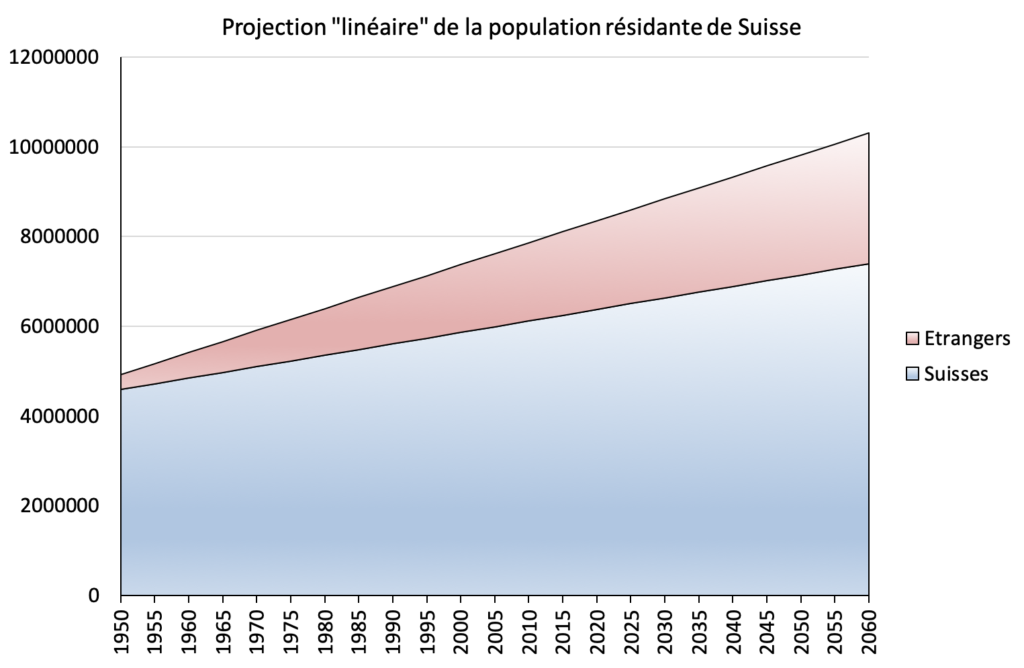
L’extrapolation « linéaire » suppose que l’augmentation annuelle de population est constante. A partir des 69 années connues, de 1950 à 2018, nous faisons l’hypothèse[15]Suite à un calcul de régression linéaire qui consiste à déterminer la droite qui passe au mieux par l’ensemble des points. d’une croissance annuelle de 25476 pour les suisses et de 23423 pour les étrangers, occupant les uns et les autres, le territoire suisse. La figure 32 montre les résultats qui sont loin des prédictions de l’UDC pour 2060.
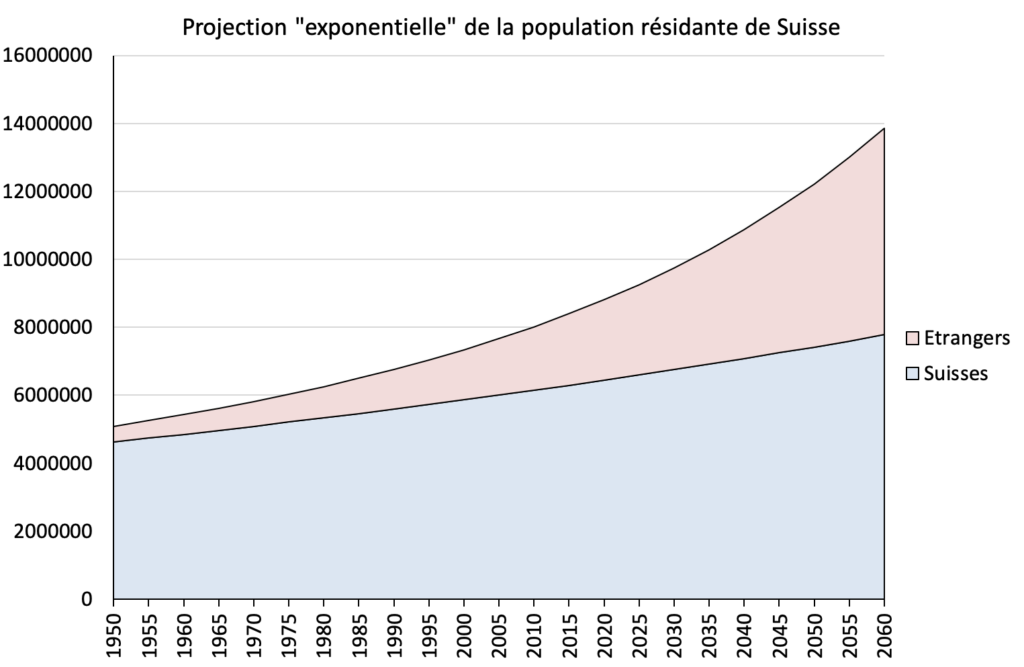
L’extrapolation « exponentielle » suppose que la population annuelle augmente chaque année d’un même pourcentage ou qu’elle est multipliée chaque année par un même facteur. Nous faisons l’hypothèse[16]Suite à un calcul de régression exponentielle qui consiste à déterminer la courbe exponentielle qui passe au mieux par l’ensemble des points. d’un facteur de croissance annuelle de 1,00473 pour les suisses (c’est-à-dire à peu près 0,5 pourcent) et de 1,02387 pour les étrangers (c’est-à-dire à peu près 2,4 pourcent). La figure 33 montre le résultat. Avec un total de 13,86 millions en 2060, cela reste encore loin des projections de l’UDC…
4 Vigilances
4.1 En bâtonnets, cartésiens
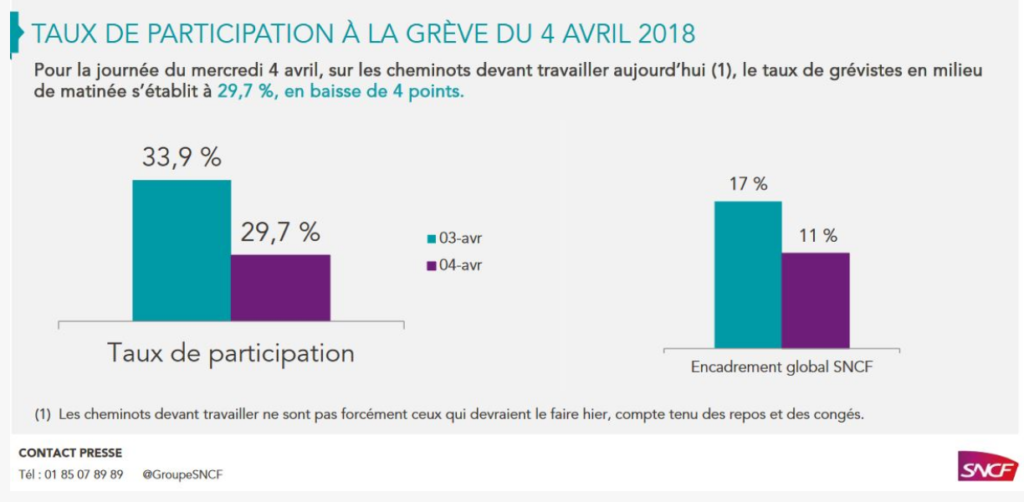
Le graphique[17]Extrait du site https://quoidansmonassiette.fr/tromper-avec-graphiques-representations-visuelles-pour-manipuler-opinion-publique-guide/. Consulté le 9 décembre 2019. de la figure 34 émane de la SNCF qui communique à propos du suivi de la grève des cheminots en avril 2018. S’agirait-il pour l’employeur de minimiser la participation de ses employés ? Les deux graphiques sont sans axes. On s’attend pourtant à une proportionnalité de la hauteur des bâtonnets aux données qu’ils représentent. Mais ce n’est pas le cas. Pour le premier graphique, il s’agit du taux de participation; pour le second, on ne sait pas trop ce qu’il a derrière « l’encadrement global SNCF ».
Le graphique[18]Extrait du site https://www.lemonde.fr/les-decodeurs/article/2018/05/22/sept-conseils-pour-ne-pas-se-faire-avoir-par-les-representations-graphiques. Consulté le 8 décembre 2019 de la figure 35 est plus explicite. Comme l’axe des ordonnées est représenté, on constate que l’origine de l’échelle n’est pas 0 mais 18 %. Avec une échelle d’origine 0, comme à la figure 36, la proportionnalité est respectée et l’impression est tout autre…
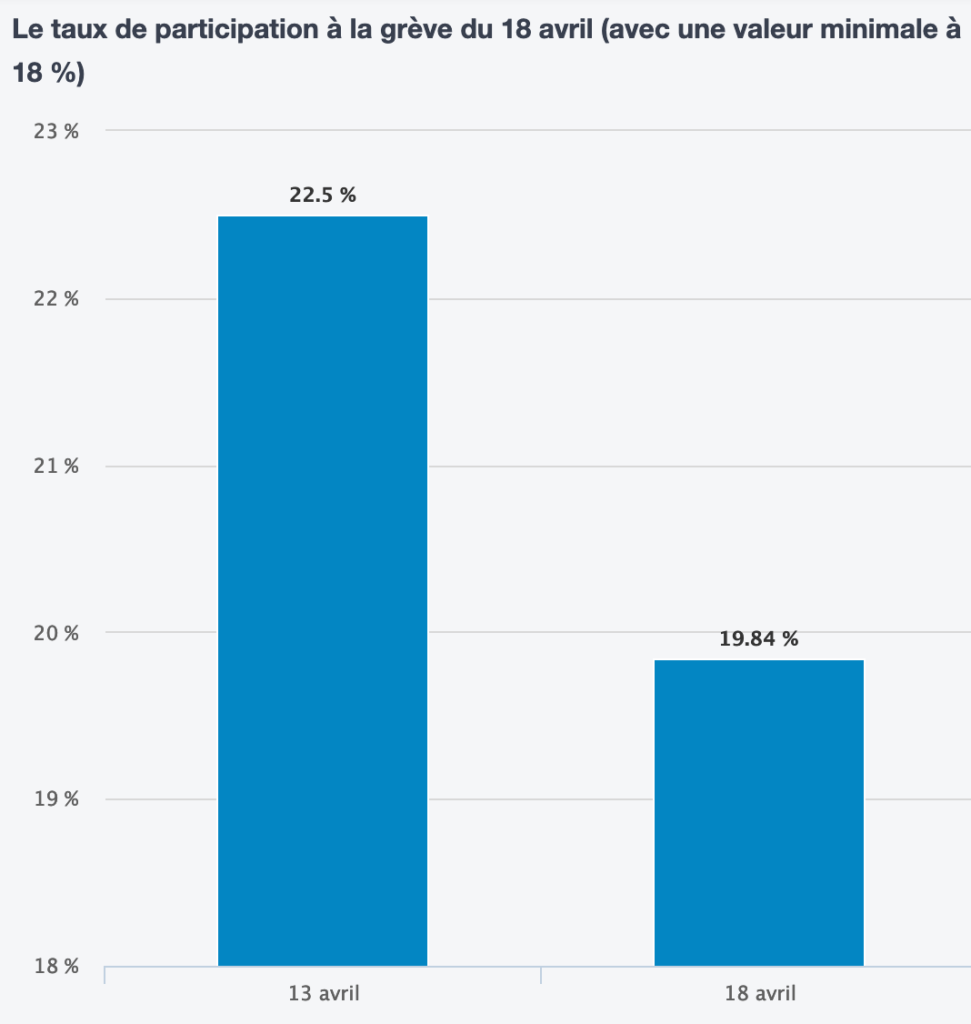
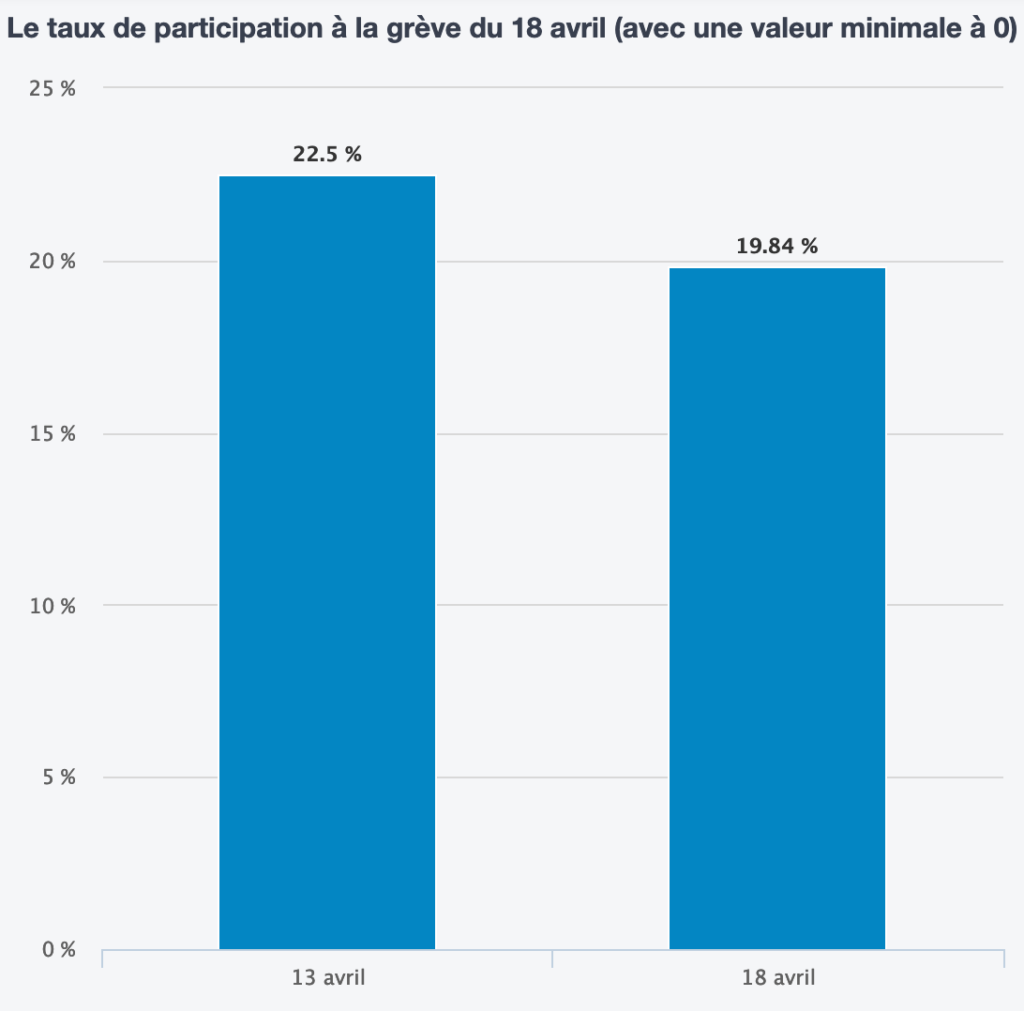
Tant pour les graphiques en bâtonnets que pour les graphiques cartésiens, il s’agit d’être attentif aux échelles (Vigilance 1) et à l’origine des axes (Vigilance 2) comme nous l’avions déjà signalé pour les figure 13 et 21.
Nous avions également relevé, en lien avec les figures 24 et 25, que selon qu’on considère des valeurs absolues ou des valeurs relatives au travers d’indices par exemple, on observe des graphiques très différents. Le graphique de la figure 37 traite également des émissions de ![]() . Mais pour l’Europe des 28, on a considéré l’évolution d’une année à l’autre. Par exemple, les émissions étaient de 3,503 billions de tonnes en 2016 et de 3,544 billions de tonnes en 2017. Ce qui nous donne un rapport d’à peu près 101,16 % ou une augmentation de 1,16 %. Ce graphique qui évoque pour l’Europe des 28, la même réalité que ceux des figures 24 et 25, est bien singulier.
. Mais pour l’Europe des 28, on a considéré l’évolution d’une année à l’autre. Par exemple, les émissions étaient de 3,503 billions de tonnes en 2016 et de 3,544 billions de tonnes en 2017. Ce qui nous donne un rapport d’à peu près 101,16 % ou une augmentation de 1,16 %. Ce graphique qui évoque pour l’Europe des 28, la même réalité que ceux des figures 24 et 25, est bien singulier.
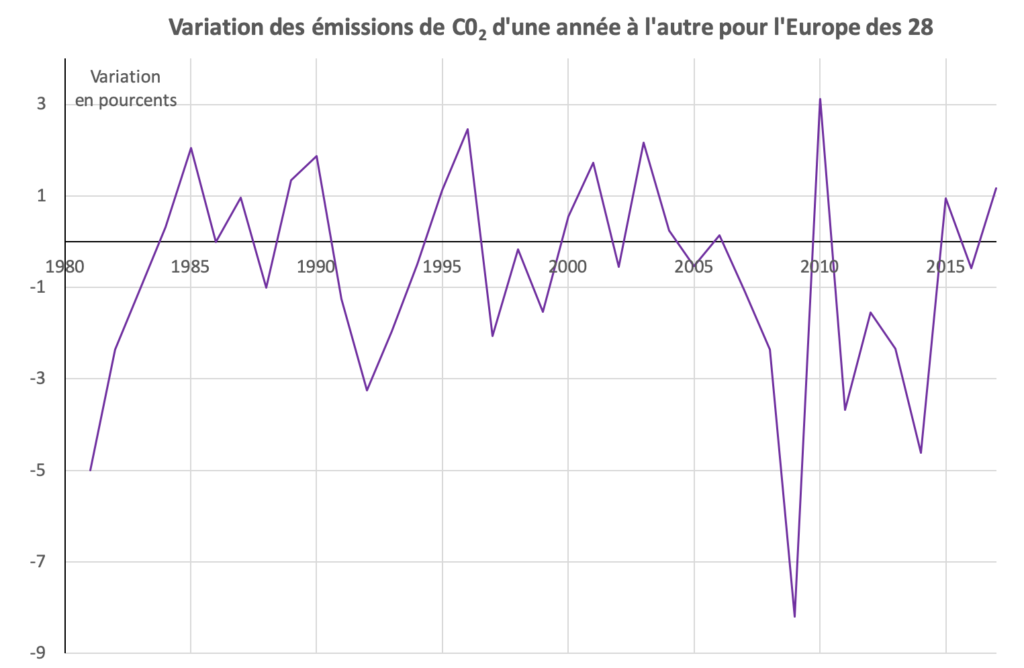
Méfions-nous donc des graphiques qui représentent des tendances, des variations, des valeurs relatives plutôt que les les valeurs absolues, et qui quelquefois trichent avec la base 100 (Vigilance 3).
Les graphiques des figures 25 et 26 soulevaient également la question de la comparaison de chiffres liés à des réalités différentes. Même si les émissions de ![]() de la Belgique et de la Chine ont en commun d’être nationales et globalisées sur l’année, elles ne sont pas comparables. Un pays de 10 millions d’habitants n’a rien à voir avec un pays qui dépasse 1,3 milliards d’habitants. Attention aux données brutes qui ne sont pas comparables (Vigilance 4).
de la Belgique et de la Chine ont en commun d’être nationales et globalisées sur l’année, elles ne sont pas comparables. Un pays de 10 millions d’habitants n’a rien à voir avec un pays qui dépasse 1,3 milliards d’habitants. Attention aux données brutes qui ne sont pas comparables (Vigilance 4).
Pour les graphiques cartésiens, à partir de la figure 12, nous avons enfin soulevé le problème des points qu’on peut relier ou non (Vigilance 5). A partir des figures 30 à 33, nous avons remis en cause l’usage maladroit ou malhonnête de modèles linéaire ou exponentiel (Vigilance 6).
4.2 Aires
Le graphique[19]BFMTV du 25 avril 2018,https://www.lemonde.fr/les-decodeurs/article/2018/05/22/sept-conseils-pour-ne-pas-se-faire-avoir-par-les-representations-graphiques. Consulté le 10 décembre 2019. de la figure 38 illustre à nouveau un problème de proportionnalité mais dans le cadre d’un graphique circulaire. 48 %, cela ne fait pas plus que la moitié. Selon les auteurs, l’erreur viendrait d’un problème de logiciel qui n’aurait pas réparti correctement les pourcentages.
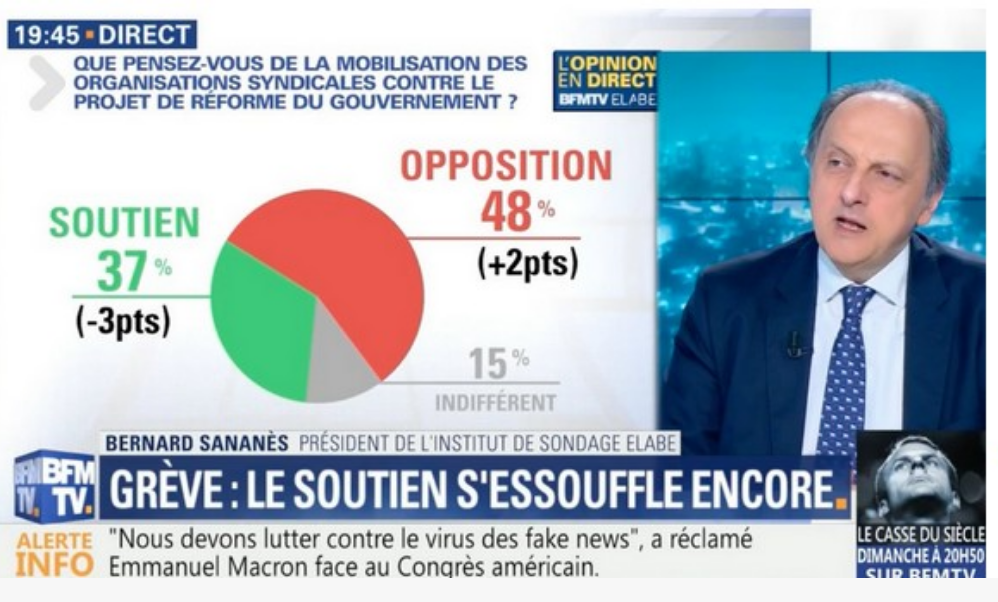
Comme nous l’avions déjà signalé, pour les graphiques circulaires, il faut s’assurer que le total des fréquences[20]Faut-il rappeler que la fréquence d’une valeur prise par une variable ou d’une modalité est le rapport entre l’effectif de cette valeur et l’effectif total. qui apparaissent, soit bien égal à 100 % et que chaque angle de secteur angulaire soit proportionnel à la fréquence qu’il représente (Vigilance7).
A la figure 15, nous avons mis le lecteur en garde contre un autre piège des graphiques circulaires en 3D qui surreprésentent certaines valeurs (Vigilance 8). Et encore, ce que nous avons montré, n’était qu’une perspective axonométrique du disque et du cylindre. Cette dernière conserve le centre du disque. Ce qui n’est pas le cas d’une perspective classique ou « à points de fuite » comme vous pouvez le constater à la figure 39.
Nous avons encore souligné l’ambiguïté de certains graphiques quant aux différences de perception qu’ils engendrent suivant qu’on considère des aires ou des longueurs (Vigilance 9). Aux figures 20 et 21, ce sont des aires qui « sautent » aux yeux et trompent le lecteur, alors que ce sont des longueurs (ou des hauteurs) qui sont significatives.
Pour des courbes « cumulées » comme aux figures 18, 19 ou 31, on colorie l’aire entre deux courbes. Attention, il s’agit à nouveau d’un piège possible (Vigilance 10). Comme nous le prouvons en annexe B, à la figure 18, l’aire entre courbes cumulées a tout son sens. Alors, qu’à la figure 19, elle n’en pas et donne un caractère trompeur au graphique. Aux figures 31 à 33, l’aire entre deux courbes n’a pas de sens mais ne trompe pas le lecteur. Certains diront même que dans ces derniers cas, cela facilite la lecture.
5 Annexes
5.1 Affinités et indices
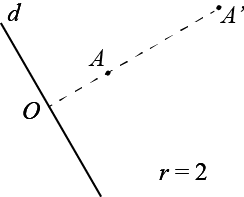
On considère une droite ![]() dans un plan, le point
dans un plan, le point ![]() et la perpendiculaire à
et la perpendiculaire à ![]() issue de
issue de ![]() . Si
. Si ![]() est le point d’intersection de
est le point d’intersection de ![]() et de la perpendiculaire, l’affinité de droite
et de la perpendiculaire, l’affinité de droite ![]() et de rapport
et de rapport ![]() (figure 40), fait correspondre à un point
(figure 40), fait correspondre à un point ![]() du plan, le point
du plan, le point ![]() tel que
tel que ![]()
Communément, on parle parfois de contraction ou de dilatation suivant que le rapport ![]() est plus petit ou plus grand que 1.
est plus petit ou plus grand que 1.
Une image de ce qu’est l’affinité est donnée par la bande élastique qu’on étire ou qu’on contracte dans la direction de sa longueur sans que sa largeur change.
Un indice exprime la variation d’une grandeur ou d’une variable par rapport à une période de référence. Considérons la production annuelle de ![]() de la Chine par exemple. Si on la note
de la Chine par exemple. Si on la note ![]() et qu’on choisit l’année 1980 comme année de référence alors l’indice vaut
et qu’on choisit l’année 1980 comme année de référence alors l’indice vaut ![]() . De cette expression, on peut conclure que par rapport au graphique de
. De cette expression, on peut conclure que par rapport au graphique de ![]() , celui de
, celui de ![]() subit une affinité d’axe
subit une affinité d’axe ![]() (ou axe des abscisses) parallèlement à l’axe
(ou axe des abscisses) parallèlement à l’axe ![]() (ou axe des ordonnées) et de rapport
(ou axe des ordonnées) et de rapport ![]() .
.
5.2 Aire sous la courbe
Revenons au graphique de la figure 18 et considérons l’aire « orange ». Le segment ![]() (figure 41) correspond à la production totale annuelle de
(figure 41) correspond à la production totale annuelle de ![]() des pays d’Europe hors Europe des 28. Soit
des pays d’Europe hors Europe des 28. Soit ![]() cette production qui vaut à peu près 2,2 millions de tonnes. Le segment
cette production qui vaut à peu près 2,2 millions de tonnes. Le segment ![]() correspond à
correspond à ![]() qui vaut à peu près 2,26 millions de tonnes. L’aire du trapèze
qui vaut à peu près 2,26 millions de tonnes. L’aire du trapèze ![]() est égale à
est égale à
(1) ![]()
sachant que la hauteur du trapèze est 1. L’aire totale orange entre 1950 et 2017 est donc égale à
(2) ![]()
(3) ![]()
L’aire totale orange correspond donc presque à la production totale de
Notes
| ↑1 | Dans certains pays comme le Québec, on parle également de graphique à bandes. |
|---|---|
| ↑2 | Selon « Permis de conduire-Online à l’adresse https://www.permisdeconduire-online.be/snelheidwet6.htm. Consulté le 8 décembre 2019. |
| ↑3 | Voir l’annexe A pour en savoir plus sur l’affinité. |
| ↑4, ↑8 | Source des données : Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019. |
| ↑5 | Extrait du site Our World in Data à l’adresse https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions. Consulté le 10 novembre 2019. |
| ↑6 | Source des données : Statbel à l’adresse https://statbel.fgov.be/fr/themes/menages/revenus-fiscaux/plus. Consulté le 10 novembre 2019. |
| ↑7 | Car il faut savoir que les 547750 ménages qui ont un revenu net imposable nul, ne sont pas repris dans l’étude… |
| ↑9 | La notion d’indice est développée à l’annexe A. |
| ↑10 | Alexandre Pouchard, Le Monde du 15 mars 2015 à l’adresse https://www.lemonde.fr/les-decodeurs. Consulté le 11 novembre 2019 |
| ↑11 | Alexandre Pouchard, Le Monde du 15 mars 2015 |
| ↑12 | Il s’agit d’un parti d’extrême droite contrairement à ce que laisse croire son appellation. |
| ↑13 | Postée le 14 janvier 2014 par Lionel Baland, l’actualité des partis patriotiques en Europe à l’adresse http://lionelbaland.hautetfort.com/archive/2014/01/17/bientot-plus-d-etrangers-que-de-suisses-5274516.html. Consulté le 19 novembre 2019. |
| ↑14 | Elles viennent de l’Office fédéral de la statistique de la Confédération suisse à l’adresse https://www.bfs.admin.ch/bfs/fr/home/statistiques/population/effectif-evolution/age-etat-civil-nationalite.assetdetail.9466966.html. Consulté le 19 novembre 2019. |
| ↑15 | Suite à un calcul de régression linéaire qui consiste à déterminer la droite qui passe au mieux par l’ensemble des points. |
| ↑16 | Suite à un calcul de régression exponentielle qui consiste à déterminer la courbe exponentielle qui passe au mieux par l’ensemble des points. |
| ↑17 | Extrait du site https://quoidansmonassiette.fr/tromper-avec-graphiques-representations-visuelles-pour-manipuler-opinion-publique-guide/. Consulté le 9 décembre 2019. |
| ↑18 | Extrait du site https://www.lemonde.fr/les-decodeurs/article/2018/05/22/sept-conseils-pour-ne-pas-se-faire-avoir-par-les-representations-graphiques. Consulté le 8 décembre 2019 |
| ↑19 | BFMTV du 25 avril 2018,https://www.lemonde.fr/les-decodeurs/article/2018/05/22/sept-conseils-pour-ne-pas-se-faire-avoir-par-les-representations-graphiques. Consulté le 10 décembre 2019. |
| ↑20 | Faut-il rappeler que la fréquence d’une valeur prise par une variable ou d’une modalité est le rapport entre l’effectif de cette valeur et l’effectif total. |