De quoi s’agit-il ?
Dans un premier temps les enfants ont déjà représenté différentes quantités (pas nécessairement organisées) de…
Dans cette activité, ils devront représenter et se représenter les schèmes du dé afin de percevoir les nombres de plus en plus rapidement. Dans un deuxième temps, nous abordons les relations entre les premiers nombres, la décomposition/recomposition facilitées par la vision globale qu’offrent les schèmes.
Enjeux
(issus du référentiel des compétences initiales)
- Savoir-faire en nombres et opérations : dénombrer une collection d’objets pour s’initier à l’aspect cardinal des nombres.
- Énoncer le mot nombre correspondant à la collection d’objets.
- Savoir-faire en nombres et opérations : composer par manipulation une quantité d’objets (jusqu’à 6) en combinant deux termes ou plus. Dire les mots nombres correspondant aux différentes compositions.
- Savoir-faire en nombres et opérations : décomposer par manipulation, une quantité d’objets définie par l’enseignant (jusqu’à 6) en deux termes ou plus, et la recomposer.
- Opérer au départ d’une collection d’objets donnée : une addition/une soustraction.
- Savoirs en nombres et opérations : reconnaitre globalement et immédiatement des représentations structurées jusqu’à 6.
De quoi a-t-on besoin ?
Pour les étapes 1 et 2, par enfant :
- un carton carré (par exemple un sous-bock, un dessous de verre),
- minimum 6 jetons.

Pour les étapes suivantes :
- Pour l’enseignant, les schèmes représentés en grand sur papier cartonné et sur feuille de plastique transparent.
- Pour les élèves, le même matériel réduit du format A4 au format A5 afin que le matériel ne prenne pas trop de place sur le banc. Les enfants travaillent sur le support de feuille A4 blanc dont la moitié est couverte par les schèmes habituels, l’autre moitié servant de support pour les nouvelles dispositions (voir photo).
Note : on peut utiliser du papier calque plastifié ou les feuilles transparentes utilisées avec les rétroprojecteurs, elles peuvent passer à la photocopieuse.



Comment s’y prendre ?
Étape 1
L’enseignant montre des schèmes du dé, les nomme, montre autant de doigts.
Il verbalise ou fait verbaliser la position des jetons. Par exemple, « 4, c’est un jeton dans chaque coin, c’est deux colonnes de 2 », « 5, c’est comme une croix, c’est comme un 4 avec un jeton au milieu », « 6, c’est deux lignes de 3 »). Il invite les élèves à mettre cette position dans leur tête afin de pouvoir la reproduire. Ensuite il cache son modèle et demande aux enfants de placer leurs jetons de la même manière sur le carton. Dans cette première étape, le carton est vidé de ses jetons entre chaque exercice. Après avoir fait de même avec les six nombres, l’enseignant ne montre plus le modèle et demande aux enfants de placer X jetons sur leur carton selon la disposition du dé.

Étape 2
- Ici on met en évidence les changements nécessaires pour passer de la représentation d’un nombre à l’autre : l’enseignant demande aux élèves de placer par exemple 2 jetons comme sur le dé. Il demande ensuite aux enfants ce qu’il faut faire pour représenter le 3 sans enlever les deux jetons : « il faut ajouter un jeton». « Et pour repasser ensuite du 3 au 2, il faudra enlever un jeton. »
On passe du 4 au 5 et du 5 au 4 de la même manière.
« Si j’ai 2 et que je veux avoir 4, je devrai ajouter 2. De même, j’ajoute 2 pour passer du 1 au 3. »
Note d’attention : certains passages sont plus complexes que d’autres si on veut retrouver les schèmes classiques du dé. Et si les élèves sont très à l’aise avec l’ajout d’un jeton pour passer d’un schème à l’autre, ils peuvent également prendre conscience que dans certains cas il faut déplacer un jeton (pour passer du 3 au 4 ou du 5 au 6).

Étape 3
Les jetons sont rangés et les élèves reçoivent les schèmes du dé sur feuille de papier et sur papier transparent (voir fichier en annexe). On peut profiter de la feuille en commençant par un petit jeu de rapidité permettant d’asseoir les précédents apprentissages : « le plus rapidement, montrez-moi sur la feuille où est le … »
Lors de cette nouvelle étape, les passages d’un nombre à l’autre se font par superposition.
Attention, une petite règle s’impose : on ne peut pas couvrir un point par un autre point !
L’enseignant propose aux élèves de poser le transparent 1 sur le transparent 2, les enfants observent le résultat : ça donne le schème de 3. Ensuite l’enseignant demande aux élèves s’ils ont d’autres idées d’assemblage.
Une fois qu’un élève exprime une idée, les autres l’imitent et posent le transparent comme lui.



- Pour passer de 2 à 3, on superpose le 1 au 2.
Mais pour obtenir ce 3, on peut aussi superposer le 2 au 1. - Et inversement quand j’ai obtenu 3 par superposition, si je retire 1 il reste 2. Si je retire le 2 il reste le 1.
- Pour passer de 4 à 5, on ajoute également 1 au centre.
- En superposant convenablement deux schèmes 2, on obtient 4.
- En posant convenablement le 2 sur le 3 ou le 3 sur le 2, on obtient 5.
- Le 1 sur le 6 et le 6 sur le 1 ça fait 7 (même si on ne le trouve pas sur le dé).






L’enseignant souligne les liens entre les différentes propositions, il dit à Marion : « tu proposes de mettre le 4 sur le 1, ça fait 5 et tout à l’heure Xavier nous a proposé de mettre le 1 sur le 4 et cela faisait également 5 ». « C’est l’inverse ! » dit Marion., « C’est parce que ce sont les mêmes nombres ! » dit Caroline.
Étape 4
À un moment les enfants se rendent compte que certaines configurations posent des difficultés avec ce matériel, on peut dans ce cas proposer des transparents avec des versions différentes du 1, 2 et 3 (voir ci-dessous)
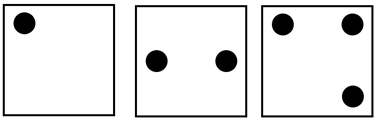


- Avec une nouvelle version du 2, on peut passer du 4 au 6.
- En prenant deux exemplaires de la nouvelle présentation du 1, on peut obtenir 2.
- Avec la nouvelle version du 3 et celle du 1, on peut obtenir 4.
- Nous avions obtenu une représentation du 3 oblique comme sur le dé en superposant le 2 et le 1; maintenant si on pose le nouveau 2 sur l’ancien 1, ça fait un 3 horizontal.
« Ou avec le nouveau 2, ça fait les oreilles et le nez de Mikey ! » - On peut également obtenir une autre disposition du 4 en superposant le 2 du dé et le nouveau 2.
- En superposant trois représentations du 2, on obtient 6.
- Passer de 5 à 6 est difficile, même avec ce nouveau matériel. On pourrait l’obtenir avec les nouveaux 1,2 et 3.






Étape 5
L’enseignant désigne un nombre et les élèves doivent, par manipulation, superposer des schèmes pour arriver à représenter ce nombre selon la configuration du dé.
On partage et on compare ensuite les démarches de chacun
(ex : 5 peut être représenté avec 1 et 4, 4 et 1, 3 et 2 ou 2 et 3).

Étape 6
L’enseignant demande ensuite aux élèves de trouver différentes configurations (autres que celle du dé) pour un même nombre :
« 4 peut être représenté avec un point dans chaque coin mais comment pourrait-on représenter 4 autrement ? »
Les élèves expérimentent puis verbalisent.

Étape 7
Après ces différentes étapes, les élèves sont amenés à dessiner schématiquement une situation vécue, ou plusieurs pour les enfants plus rapides : ils doivent dessiner de manière simplifiée pour progresser vers l’abstraction.
Ensuite, une dictée à l’adulte encouragera l’enfant à mettre des mots sur les actions dessinées.
On compilera les différents dessins pour garder une trace.
Premiers essais

Deuxième essai


Étape 8
Il s’agit de garder une trace des différentes représentations rencontrées d’un même nombre. Exemple de différentes manières de constituer 4 :




Échos d’une classe
Les élèves sont très actifs, certains essaient d’anticiper.
D’une séance à l’autre on peut les observer progresser, chacun à son niveau.
Prolongements
En cherchant différentes possibilités, les enfants en viennent à superposer plus de deux schèmes et ainsi additionner trois nombres : 2+2+1=5 .
Vers où cela va-t-il ?
Ce travail aide les élèves
- À se faire une image des nombres,
- À créer des liens entre les nombres : liens d’inclusion (dans deux nombres consécutifs, il y en a un inclus dans l’autre, ils sont liés par la relation +1/-1) et lien de composition/décomposition (tout nombre peut être décomposé à l’aide des nombres précédents).
- À appréhender l’addition.
Commentaires
Cette activité s’étale sur plusieurs séances afin de bien faire intégrer les notions.
Il est important de bien verbaliser ainsi que d’encourager les enfants à « mettre dans leur tête » afin de progressivement arriver à reconnaitre globalement ces représentations structurées. Grâce à ce travail, les élèves pourront reconnaitre une quantité sans compter par un. Ils doivent comprendre qu’une collection bien organisée (par exemple la constellation du dé) nous permet de voir très vite « combien il y en a », qu’il est plus efficace de voire globalement que de compter un à un. Le fait d’organiser permet également de mieux « voir » les liens : dans le 5 du dé, on peut voir le 4 et le 1 ; le schème 6 nous montre les 2×3.
Mais les élèves doivent aussi savoir que le schème du dé n’est pas la seule représentation du nombre ; il faudra également travailler sur différentes dispositions du nombre.
Il est préférable d’introduire les schèmes spéciaux dans un deuxième temps, lorsque les enfants se rendent compte par eux-mêmes de l’impossibilité de réaliser certaines représentations sans eux.
