Comprendre et interpréter les graphiques des cas covid placés dans un système d’axes semi-logarithmique

Cet article a pour but de mettre en place les connaissances nécessaires pour comprendre le fonctionnement des graphiques des cas de Covid-19 qui sont placés dans un système d’axes semi-logarithmique. Ces connaissances comportent plusieurs propriétés des fonctions exponentielles et logarithmiques.

1. Que signifie l’expression « croissance exponentielle » ?

Au début de la pandémie, certains chercheurs ont redouté que la propagation de Covid-19 ait une croissance exponentielle en se référant aux données présentées par le diagramme reproduit ci-dessous.(https://www.sciencesetavenir.fr/fondamental/mathematiques/covid-19-une-croissance-exponentielle_142539). Cette croissance est très rapide. Mais, s’agit-il ici vraiment d’une croissance exponentielle?

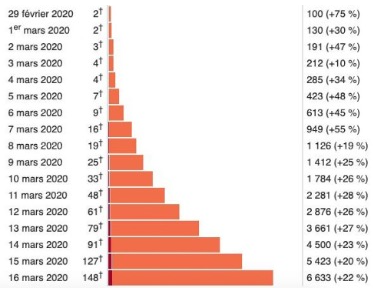
Le diagramme de la figure 1 est établi, à partir des données numériques journalières du nombre total de malades de Covid-19, par les calculs selon la formule

$\frac{P(n+1)-P(n)}{P(n)} \times 100 .$

Dans cette formule, la lettre $n$ désigne le nombre de jours et la notation $P(n)$ désigne le nombre total de malades de Covid-19 le n^ejour. L’expression $\large{\frac{P(n+1)-P(n)}{P(n)}}$ s’appelle le taux de croissance journalier ou le rythme journalier de croissance.

Remarquons que ce diagramme ne respecte pas la convention adoptée en mathématiques de représenter la variable indépendante sur l’axe horizontal et la variable dépendante sur l’axe vertical, ce qui est corrigé à la figure 2. La forme du diagramme ainsi présenté suggère qu’il peut s’agir d’une croissance exponentielle. Est-ce le cas ?

Pour que la croissance des malades de Covid-19 soit considérée comme une croissance exponentielle, le taux de croissance journalier doit être constant, ce qui n’est pas vérifié ici. En effet, ce taux varie d’un jour à l’autre : 0,75 ; 0,30 ; 0,47 ; 0,10 ; 0,34 ; 0,48 ; 0,45 ; 0,55 ; 0,19 ; 0,25 ; 0,26 ; 0,28 ; 0,26 ; 0,27 ; 0,23 ; 0,20 ; 0,22.

D’une manière générale, la croissance exponentielle est définie comme une croissance dans un même rapport sur tous les intervalles de temps de même longueur $\Delta t$ , quelle que soit cette longueur : $\large{\frac{P(t + \Delta t)}{P(t)} = \frac{P(\Delta t)}{P(0)}}$ pour toutes les valeurs de $t$ et de $\Delta t$ . Cela revient à dire que la suite

$P(t)$ , $P(t + \Delta t)$ , $P(t+2 \Delta t)$ , $P(t +3 \Delta t)$ , …, $P(t +n \Delta t)$ , …

est géométrique.

Dans Grand’Henry-Krysinska et Schneider-Gilot (2017) et Henrotay et al. (2015), on établit la formule générale du type exponentiel

$P(t)=P(0)\left(\frac{P(1)}{P(0)}\right)^t$

de la fonction $P(t)$ ainsi définie et dans la section 8, on le montrera pour les valeurs rationnelles de $t$ .

2. Une « croissance exponentielle » signifie-t-elle toujours une “croissance rapide ” ?

Supposons que la population des cas de Covid-19 progresse en doublant chaque jour. Alors après 23 jours, on aurait un nombre de cas plus grand que le nombre d’habitants en Belgique. Et, 10 jours plus tard seulement, cette population pourrait atteindre théoriquement 8 589 934 592 cas, donc plus que toute la population qui vit sur la Terre. Par contre, si la population des cas de Covid-19 doublait tous les 7 jours, alors il aurait fallu 231 jours pour atteindre théoriquement le même nombre, 8 589 934 592 cas. Les deux croissances des populations sont exponentielles, mais la première peut être considérée comme extrêmement rapide et la deuxième plutôt très lente en comparaison avec la première. L’un des moyens pour comparer la vitesse de croissance d’une population est le temps de doublement dont il est question dans la section suivante.

3. Selon quelle formule évolue la croissance exponentielle d’une population qui double tous les jours ou bien tous les deux jours ou encore tous les sept jours ?

Le doublement tous les jours est illustré par le tableau suivant : $P(n)$

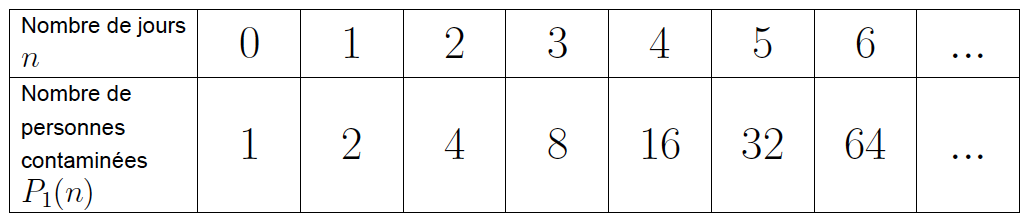
La formule associée est $P_1(n)=2^n$ .

Le doublement tous les deux jours est illustré par le tableau ci-dessous :

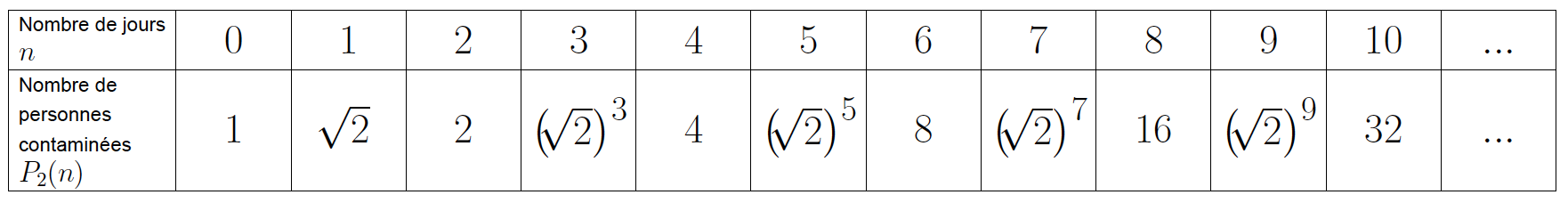
On y associe la formule $P_2(n)=\left(\sqrt{2}\right)^n = \large{2^\frac{n}{2}}$

Le doublement tous les 7 jours est illustré par le tableau ci-dessous :

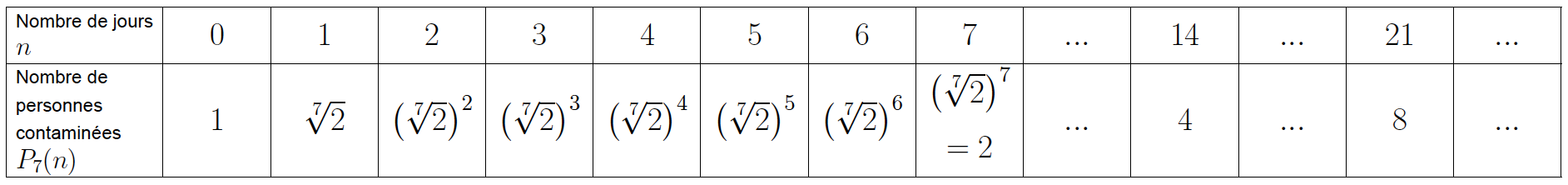
On y associe la formule $P_7(n)=\left(\sqrt[7]{2}\right)^n = \large{2^\frac{n}{7}}$

4. Quels renseignements sur l’évolution des cas de Covid-19 peut-on tirer à partir des graphiques placés dans un système d’axes uniforme ? Ces graphiques permettent-ils de comparer le rythme de croissance de l’épidémie entre des pays ?

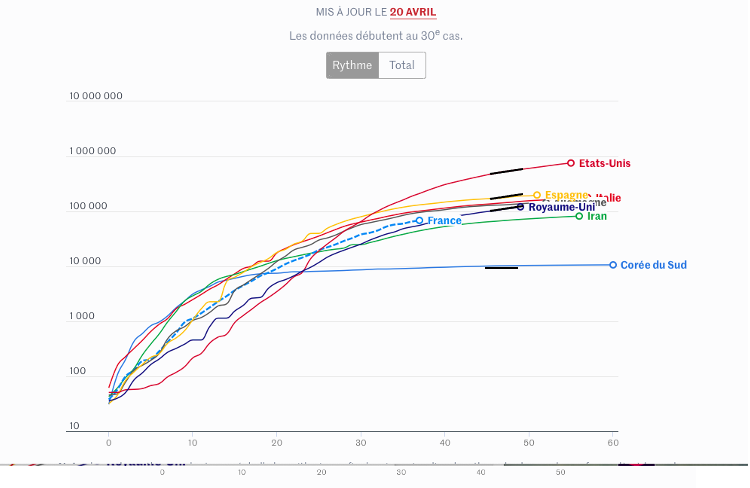
Les graphiques de la figure 3 représentent l’évolution du nombre total de cas au début de la pandémie de Covid-19, dans quelques principaux foyers (Source : Université Johns Hopkins et Santé Publique France), à partir du jour où on compte 30 nouveaux cas Covid-19 jusqu’à 55^e jour de l’épidémie.

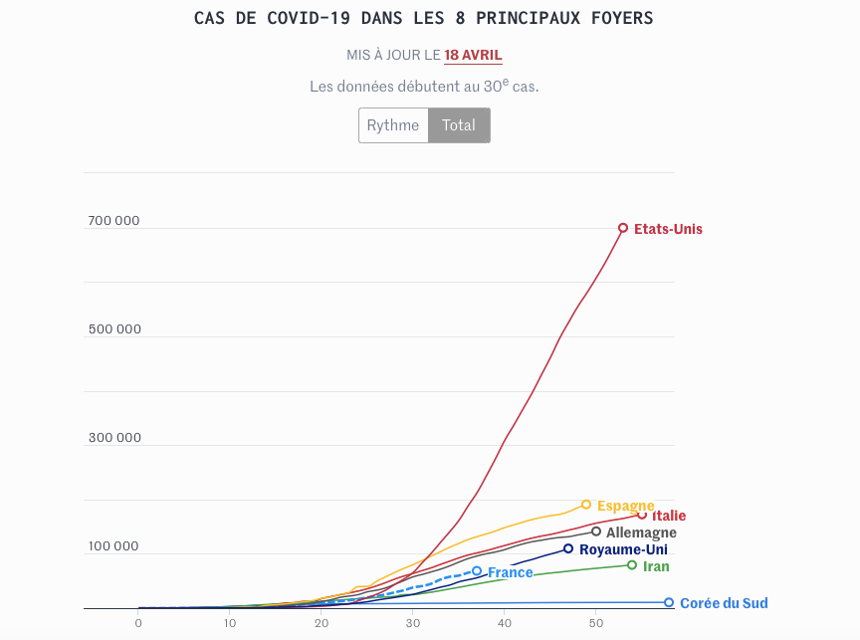
Le premier jour d’observations est différent d’un pays à l’autre car la maladie de Covid-19 ne s’est pas répandue partout en même temps. Par exemple, en Italie, elle est apparue au début du mois de février 2020, tandis qu’aux États-Unis, un mois plus tard. Sur les graphiques de la figure 3, on peut voir directement dans quel pays il y a le plus de cas, dans quel autre le moins de cas, ou si le nombre de cas est croissant ou décroissant ou s’il stagne… . Par exemple, le graphique des États-Unis comparé à ceux des autres pays suggère que ce pays est le plus affecté par le virus parce que le nombre de cas Covid-19 est en augmentation tous les jours et il arrive à 700 000 après 50 jours de la durée de la pandémie, tandis qu‘en Espagne, après la même durée, le nombre de cas s’élève à environ 150 000. En plus, lorsqu’on compare le taux d’accroissement journalier

$\frac{P(n+1)-P(n)}{1}=P(n+1)-P(n)$

en nombre des cas de Covid-19 par jour, visualisé par les pentes des segments qui semblent se confondre avec les graphiques, comme cela est illustré à la figure 4, on constate, qu’à partir du 30^e jour de la pandémie, le taux d’accroissement des cas aux États-Unis reste le plus grand par rapport à celui des autres pays.

Mais, ce n’est pas parce que le nombre de cas ou le taux d’accroissement journalier aux États-Unis est beaucoup plus grand que, par exemple, le nombre de cas ou le taux d’accroissement journalier en Italie, qu’on peut conclure que la situation sanitaire aux États-Unis est plus grave que celle en Italie. Pour le comprendre, passons aux données numériques estimées à partir des graphiques de la figure 4 concernant le nombre de cas Covid-19 le 51^e et le 52^e jour pour comparer le taux d’accroissement $\large{\frac{P(52)-P(51)}{1}}=\small{P(52)-P(51)}$ dans les cas des États-Unis et de l’ Italie.

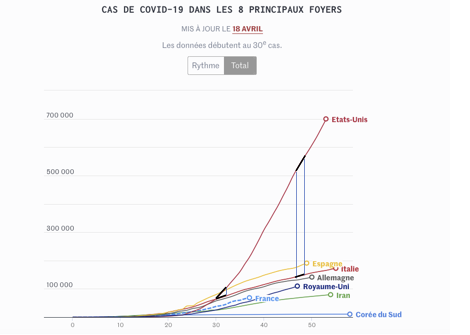
Dans le cas des États-Unis, le nombre de cas de Covid-19 du 51^e au 52^e jour passe de 650 000 à 696 000 cas, ce qui donne l’estimation du taux d’accroissement 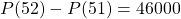$\small{P(52)-P(51)}=46 000$ cas par jour.
Dans le cas de l’Italie, le nombre de cas de Covid-19 passe de 150 000 à 163 000 ce qui donne 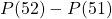$\small{P(52)-P(51)}$ estimé à 13 000 cas par jour.

La difficulté de comparer ces résultats est liée aux tailles différentes de ces deux populations des cas de Covid-19. Pour en tenir compte, il faut relativiser les données en remplaçant le taux d’accroissement journalier $\large{\frac{P(n+1)-P(n)}{1}}$ par le taux de croissance journalier défini déjà en section 1 par $\large{\frac{P(n+1)-P(n)}{P(n)}=\frac{P(n+1)}{P(n)}}-1$ , ou, si on le veut sous sa forme traduite en pourcentage, par $\left(\frac{P(n+1)}{P(n)} -1\right)\times100$ . Ce taux de croissance journalier est appelé aussi, dans différentes publications, le rythme de croissance journalier. Dans les deux cas considérés ci-dessus, on obtient le rythme de croissance égal à

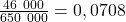$\large{\frac{46\ 000}{650\ 000}}=\small{0,0708}$ ou 7,08% des nouveaux cas par rapport aux cas de Covid-19 déjà recensés en États-Unis ;

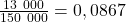$\large{\frac{13\ 000}{150\ 000}}=\small{0,0867}$ ou 8,67% des nouveaux cas par rapport aux cas de Covid-19 déjà recensés en Italie.

Il en résulte que le rythme de croissance de la maladie du 51^e au 52^e jour au États Unis est presque le même que celui en Italie, et même légèrement plus petit. La situation sanitaire est donc comparable entre ces deux pays et même elle est légèrement meilleure aux États-Unis.

D’une manière générale, la notion du rythme de croissance des cas de Covid-19 servira d’indice de l’efficacité des méthodes-barrières mises en place par un pays pour protéger sa population contre l’augmentation des cas de Covid-19. Mais, les graphiques de la figure 3 ne permettent pas de comparer ce rythme de croissance sans les calculs supplémentaires comme ceux supra.

5. Pour quelle raison place-t-on des graphiques de l’évolution des cas de Covid-19 dans un système d’axes semi-logarithmique ?

Ci-dessous, à la figure 5, sont proposés les graphiques de l’évolution du nombre total des cas de Covid-19 pendant les cinquante premiers jours de l’épidémie, pour quelques pays du monde choisis.

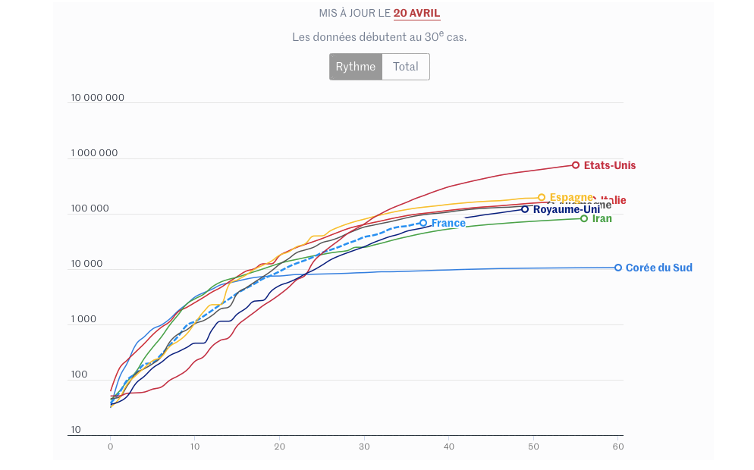
Mais le système d’axe n’est pas habituel ici car son axe vertical n’est plus gradué uniformément. En effet, sur cet axe, ce sont les puissances successives de 10 qui sont réparties uniformément. Ces puissances sont représentées par leurs exposants de 10. Or, faire correspondre à une puissance de 10 son exposant revient à considérer la fonction réciproque de la fonction exponentielle de base 10, c’est-à-dire la fonction logarithme de base 10. Il s’agit donc d’une représentation graphique dans un système d’axes semi-logarithmique. Nous allons présenter ci-dessous des raisons pour lesquelles de tels graphiques permettent de comparer à vue le rythme de croissance des cas de Covid-19 des différents pays. En effet, tous ces graphiques sont obtenus en substituant aux ordonnées des points leurs logarithmes. Ainsi, le taux d’accroissement journalier $\large{\frac{\log_{10}{P(n+1)}-\log_{10}{P(n)}}{1}}$ de $\log_{10}{P(n)}$ est lié au taux de croissance ou au rythme de croissance de $P(n)$ car $\log_{10}{P(n+1)}-\log_{10}{P(n)} = \log_{10} \large{\frac{P(n+1)}{P(n)}}$ . Les intervalles de la croissance ou de la décroissance de $\log_{10} \large{\frac{P(n+1)}{P(n)}}$ sont les mêmes que ceux de $\large{\frac{P(n+1)}{P(n)}}$ et ainsi de $\large{\frac{P(n+1)}{P(n)}-1}$ car la fonction $\log_{10}$ et sa réciproque $\exp_{10}$ sont croissantes.

D’autre part, le taux d’accroissement $\large{\frac{ \log_{10}P(n+1)-\log_{10}P(n)}{1}}$ de $\log_{10}P(n)$ peut être graphiquement interprété comme la pente d’un segment qui se confond localement, au point d’abscisse n, avec le graphique de $\log_{10}P(n)$ (figure 6).

Donc, l’évolution des pentes de ces segments d’un jour à l’autre donne l’idée de la dynamique des contagions. Lorsque le rythme est constant, on considère que la croissance est exponentielle. En effet, $\large{\frac{P(n+1)}{P(n)}}=\small{C}$ , où $\small{C}$ est une constante, équivaut à $P(n+1)=\small{C}P(n)$ , autrement dit à ce que $P(n)$ est une suite géométrique.

Le rythme de croissance journalière croissant signifie ainsi la croissance plus rapide que la croissance exponentielle. Par exemple, pendant les 10 premiers jours, le rythme de croissance journalière des cas Covid-19 aux États-Unis a été croissant, donc le nombre total des cas de Covid-19 augmentait plus vite qu’exponentiellement.

Des graphiques placés dans un système semi-logarithmique permettent aussi de relativiser la gravité de la situation dans un grand pays comme les États-Unis où, le rythme pendant les 20 derniers jours est presque égal aux rythmes des autres pays.

On peut voir aussi sur ces graphiques qu’à partir du 10^e jour d’épidémie, le rythme de croissance des cas de Covid-19 en Corée du Sud est pratiquement égal à 0 (pente du graphique nulle). Cela signifie que le nombre de cas Covid-19 y est constant. En effet, $\log_{10} \large{\frac{P(n+1)}{P(n)}}=0$ équivaut à $\large{\frac{P(n+1)}{P(n)}}=1$ et donc à $P(n+1)=P(n)$ . Cela signifie que la propagation de la maladie s’est arrêtée après les 10 premiers jours.

6. Comment peut-on estimer à vue le temps de doublement des cas dans un pays donné et à un moment donné ?

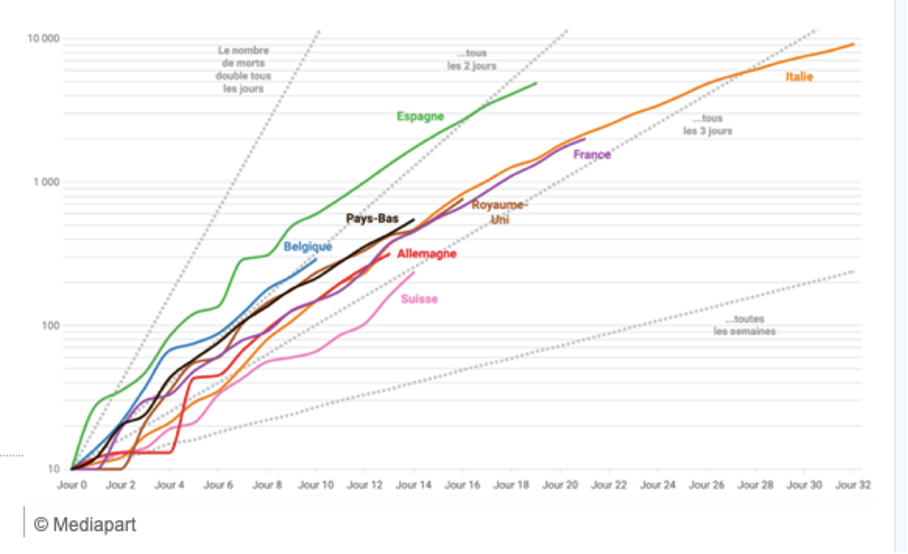
Dans la figure 7, sont repris quelques graphiques relatifs à la mortalité due au Covid-19 et les quatre droites. De quelle manière ces droites sont-elles associées au temps du doublement du nombre de morts et aident-elles à l’estimer ?

D’abord, remarquons que,dans un système semi-logarithmique, toute droite passant par l’origine est la représentation graphique d’une fonction exponentielle. En effet, l’équation $\log_{10} y=kx$ d’une droite passant par l’origine dans ce système d’axes est équivalente à l’équation $y=10^{kx}$ . Et réciproquement, les représentations graphiques des fonctions comme $P_1 (n)=2^n$ , $P_2 (n)=2^\frac{n}{2}$ , $P_3 (n)=2^\frac{n}{3}$ , $P_7 (n)=2^\frac{n}{7}$ , sont des droites. En effet, pour le montrer, nous nous appuyons sur l’identité $a=10^{\log_{10}a}$ :

$\small{\begin{array}{lllllllll}\log_{10}P_1(n) & = & \log_{10} 2^n & = & \log_{10} 10^{\log_{10}(2^n)} & = & \log_{10} 10^{n \log_{10} 2} & = & n\log_{10} 2 \\ \log_{10}{P_2 (n)} & = & \log_{10}2^\frac{n}{2} & = & \log_{10}10^{\log_{10}2^\left(\frac{n}{2} \right)} & = & \log_{10}10^{\frac{n}{2}\log_{10}2} & = & \frac{n}{2} \log_{10}2 \\ \log_{10}{P_3 (n)} & = & \log_{10}2^\frac{n}{3} & = & \log_{10}10^{\log_{10}\left(2^\frac{n}{3}\right)} & = & \log_{10}10^{\frac{n}{3}\log_{10}2} & = & \frac{n}{3} \log_{10}2 \\ \log_{10}{P_7 (n)} & = & \log_{10}2^\frac{n}{7} & = & \log_{10}10^{\log_{10}\left(2^\frac{n}{7}\right)} & = & \log_{10}10^{\frac{n}{7}\log_{10}2} & = & \frac{n}{7} \log_{10}2\end{array}}$

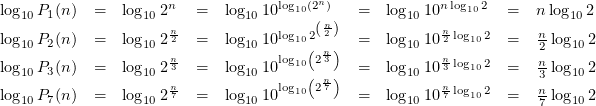
Les quatre fonctions de la variable n données par des expressions de $\log_{10}P_1(n)$ , $\log_{10}P_2(n)$ , $\log_{10} P_3(n)$ et $\log_{10} P_7 (n)$ sont linéaires et donc représentées par des droites dans le système semi-logarithmique représenté à la figure 7.

Posons, à présent, un autre regard sur les graphiques de la figure 7. Si une portion d’un graphique correspondant à un intervalle de temps est un segment qui est parallèle à l’une des droites de la figure 7, alors le temps de doublement de cas de Covid-19 sur cet intervalle correspond au temps de doublement associé à la droite. Par exemple, le graphique représentant l’évolution de cas de Covid-19 en Belgique entre le premier et le quatrième jour est presque parallèle à la droite du doublement tous les jours. Ou encore le graphique de l’Italie qui, à partir du 26^e jour, devient presque un segment de droite parallèle à la droite représentant le doublement tous les sept jours.

7. Résumé des propriétés des fonctions exponentielles et logarithmiques utilisées

Dans l’analyse des graphiques, nous nous sommes appuyés sur quelques propriétés algébriques des fonctions exponentielles et logarithmes. Citons-les ci-dessous :

la définition d’une fonction exponentielle selon laquelle toute fonction dont la croissance ou la décroissance se font dans un même rapport sur des intervalles de temps égaux ;
la définition d’une fonction logarithme comme réciproque d’une fonction exponentielle, d’où l’identité $y=\large{10^{\log_{10}y}}$ ;
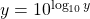l’identité $\log_{10}a-\log_{10}b = \log_{10}\large{\frac{a}{b}}$ ;
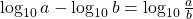la représentation graphique d’une fonction exponentielle dans un système semi-log par une droite.

Dans ce texte, nous avons fait la distinction entre le taux d’accroissement journalier appelé aussi la vitesse d’accroissement $\large{\frac{P(n+1)-P(n)}{1}}$ et le taux de croissance journalier $\large{\frac{P(n+1)-P(n)}{P(n)}}$ appelé aussi le rythme de croissance ou de décroissance journalière.

Lorsque le taux de croissance journalier est constant, alors la suite $P(n)$ est géométrique car $\large{\frac{P(n+1)-P(n)}{P(n)}}=\small{C}$ équivaut à $\small{P(n+1) = (C+1)P(n)}$ .

8. Appendice théorique : généralisation du taux de croissance journalier

Que devient le taux de croissance lorsqu’on change l’unité du temps ou l’intervalle du temps d’observation ? Par exemple, lorsqu’on observe le nombre de cas Covid-19 d’une semaine à l’autre avec l’unité du temps « un jour » ou lorsqu’on observe le nombre de cas Covid-19 d’un jour à l’autre mais l’unité du temps est « une heure » ? Pour se rendre indépendant du choix des unités et de la durée d’observation, on généralise la notion du taux de croissance journalier, on définit le taux de croissance moyen.

Le taux de croissance moyen ou le rythme de croissance moyen d’une population sur un intervalle de temps $[t,t+\Delta t]$ est défini par $\Large{ \frac{\frac{P(t+\Delta t)-P(t)}{\Delta t}}{P(t)}}$ .

Proposition

Si le taux de croissance $\Large{\mathbf{\frac{\frac{P(t+\Delta t)-P(t)}{\Delta t}}{P(t)}}}$ est constant sur tous les intervalles $\mathbf{[t,t+\Delta t]}$ , $\bf{t}$ et $\bf{\Delta t}$ réels, alors la fonction $\mathbf{P(t)}$ est exponentielle.

Preuve pour les valeurs de $t$ rationnelles :

Supposons que $\Large{\frac{\frac{P(t+\Delta t)-P(t)}{\Delta t}}{P(t)}=C_{\Delta t}}$ où $C_{\Delta t}$ est une constante qui dépend seulement de la valeur de $\Delta t$ . Cela signifie que :

(1) $\begin{equation*}P(t+\Delta t)=(\Delta t\cdot C_\Delta t+1)P(t) \end{equation*}$

Ainsi

(2) $\begin{equation*}P(1)=(C_1+1)(P(0) \end{equation*}$

ou bien

(3) $\begin{equation*}C_1+1=\frac{P(1)}{P(0)} \end{equation*}$

Posons ensuite $t=\frac{k}{n}$ , $\Delta t = \frac{1}{n}$ et appliquons l’égalité (1) $k$ fois :

$\begin{array}{rcl}P(\frac{k}{n}) & = & P\left(\frac{k-1}{n}+\frac{1}{n}\right) \\& = & \left(\frac{1}{n}C_\frac{1}{n}+1\right)P\left(\frac{k-1}{n}\right) \\& = & \left(\frac{1}{n}C_\frac{1}{n}+1\right)^2P\left(\frac{k-2}{n}\right) \\& = & \left(\frac{1}{n}C_\frac{1}{n}+1\right)^3P\left(\frac{k-3}{n}\right) \\& = & ... \\& = & \left(\frac{1}{n}C_\frac{1}{n}+1\right)^kP(0) \end{array}$

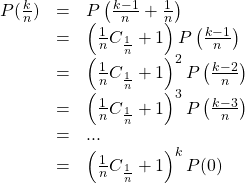
Plus particulièrement, pour $t=1$ et $k=n$ , on obtient

$P(1)=\left(\frac{1}{n} C_\frac{1}{n}+1\right)^n P(0)$

D’où, par (2)

$\left(\frac{1}{n} C_\frac{1}{n}+1\right)^n =C_1+1.$

En appliquant (3), on obtient finalement

$P\left(\frac{k}{n}\right)=( C_1+1)^\frac{k}{n} P(0)=\left( \frac{P(1)}{P(0)}\right)^\frac{k}{n} P(0)$

Ainsi, le caractère exponentiel de $P(t)$ est démontré pour les valeurs rationnelles positives de $t$ . Le passage aux valeurs irrationnelles se fait à l’aide des l’axiomes de complétude et d’Archimède.

9. Taux de croissance comme pente de tangente au graphique d’une fonction donnée par $P(t)$ et placé dans un système semi-logarithmique

Considérons un taux de croissance moyen

$\large{\frac{\frac{P(t+\Delta t)-P(t)}{\Delta t}}{P(t)}}.$

Sa limite

$\large{\lim_{\Delta t\to 0}\frac{\frac{P(t+\Delta t)-P(t)}{\Delta t}}{P(t)}=\frac{P'(t)}{P(t)}}$

est considérée alors comme un taux de croissance instantané ou encore le rythme de croissance instantané en $t$ d’une population donnée $P(t)$ .

Comme on a aussi $\large{\frac{P'(t)}{P(t)}=\left(\ln{P(t)}\right)'}$ , l’expression $\large{\frac{P'(t)}{P(t)}}$ est à la fois celle de la pente d’une tangente en $t$ de la courbe représentant la fonction $\ln{P(t)}$ et d’un taux de croissance instantané en $t$ d’une population donnée $P(t)$ . Ce fait justifie largement l’intérêt d’utiliser le système semi-logarithmique pour représenter la variation d’une population donnée en fonction du temps. On peut ainsi interpréter le taux de croissance instantané $\large{\frac{P'(t)}{P(t)}}$ comme pente de la tangente au graphique de $\ln{P(t)}$ , c’est-à-dire au graphique de $P(t)$ placé dans un système d’axes semi-logarithmique.

9. Références

Grand’Henry-Krysinska M., Schneider-Gilot M., Genèse du modèle exponentiel, Petit x n° 105, 2017,

Henrotay P., Krysinska M., Rossel H., Schneider M., Des fonctions taillées sur mesure :construire les fonctions sinusoïdales, exponentielles et logarithmes pour modéliser des problèmes variés, Presses Universitaires de Liège, 2015

Partager :