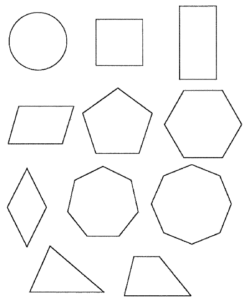
Comment couper en deux parties « égales » un disque, un carré, un rectangle et quelques autres formes géométriques communes ? Bien que ce thème de réflexion soit tout à fait élémentaire, nous proposons au lecteur de s’y arrêter un moment, ciseaux en main. Les formes à couper en deux sont celles de la figure ci-contre. L’idée est de laisser courir son imagination pour voir de quels apprentissages géométriques ce thème est porteur.
Une fois cette exploration terminée, le lecteur est invité à raconter sa démarche par écrit en expliquant non seulement les phénomènes mathématiques rencontrés, mais aussi les péripéties de sa pensée en recherche ; conjectures, exemples, contre-exemples, points de méthode réinvestissables dans d’autres explorations, surprises, espoirs, fatigue, contentement.
Ceci fait, il pourra lire la suite du texte et s’apercevra, c’est certain, qu’il a découvert des choses auxquelles l’auteur n’a pas pensé, et réciproquement. Il pourra aussi, s’il est enseignant, s’inspirer de ce qu’il aura fait et lu pour stimuler ses élèves. Bien entendu, rien n’empêche le lecteur pressé de court-circuiter toutes ces propositions et de prendre d’emblée connaissance du texte.
Cet article a été publié dans la brochure suivante : – Cellule de pilotage, Secrétariat général, Ministère de l’Éducation, de la Recherche et de la Formation, Mathématiques de 10 à 14 ans, Continuité et compétences, 1996, D/1996/7224/2. Le document complet est disponible en téléchargement en version PDF (voir ci-dessous).