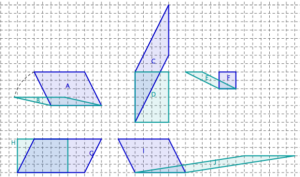
On utilise les familles de parallélogrammes pour comparer et déformer des figures tout en travaillant les notions d’aire et de périmètre. Le matériel utilisé dans les activités précédentes constitue une aide pour les activités ci-dessous.
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Figures de même famille ?
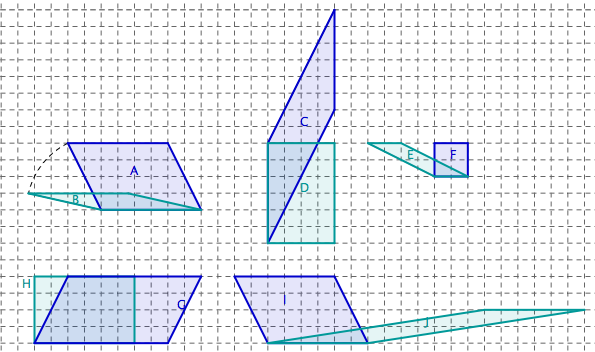
Comparez, sans les calculer, l’aire et le périmètre des figures deux par deux.
Solutions
Comparaison des parallélogrammes A et B. Ils ont le même périmètre. On peut, pour s’en convaincre, évoquer le matériel « Tiges articulées » de l’article Familles de parallélogrammes.
Par contre, l’aire de B est plus petite que celle de A. En effet, ils ont la même base mais la hauteur de B est plus petite.
Comparaison des parallélogrammes C et D. Ils ont la même aire. On peut, pour s’en convaincre, évoquer le matériel « Tubes qui coulissent » de l’article Familles de parallélogrammes en tenant les tiges verticalement. Ils ont la même base (verticale) et la même hauteur (horizontale). Il est nécessaire de changer de point de vue pour le voir.
Par contre, le périmètre de C est plus grand que celui du rectangle D. En effet, leurs côtés verticaux sont de même longueur mais les côtés obliques de C sont plus longs que les côtés horizontaux de D.
Comparaison des parallélogrammes E et F. Ils ont la même aire et leurs périmètres sont différents. La justification est la même que dans le cas précédent. Ici, la base commune étant horizontale, la comparaison des aires est plus spontanée.
Comparaison des parallélogrammes H et G. L’aire de G est plus grande que celle de H. En effet, ils ont même hauteur mais la base de G est plus grande que celle de H.
De même, le périmètre de G est plus grand que celui de H. En effet, les côtés horizontaux de G sont plus longs que ceux de H et ses côtés obliques sont plus longs que les côtés verticaux de H.
Comparaison des parallélogrammes I et J. L’aire de I est plus grande que celle de J. En effet, ils ont même base mais la hauteur de I est plus grande que celle de J.
Par contre, le périmètre de J est plus grand que celui de I car leurs côtés horizontaux ont même longueur mais les côtés obliques de J sont plus longs que ceux de I.
Comparer le périmètre et l’aire
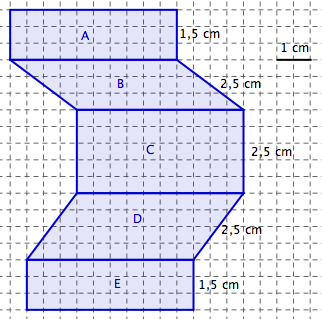
Comparez le périmètre des figures A, B, C, D, E sans calculer. Faites ensuite de même pour l’aire.
Solutions
Périmètres. Les figures B, C et D ont le même périmètre. Celui-ci est plus grand que celui des figures, superposables, A et E.
Aires. Les figures A, B et E ont la même aire (même base et même hauteur). Celle de D est plus grande, et celle de C encore plus.
Comparaison de deux aires
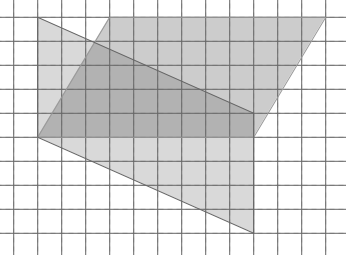
Sans rien mesurer, sans calculer, déterminez quel parallélogramme a l’aire la plus grande.
Solutions
Plusieurs procédures sont possibles. Certaines consistent à comparer ces deux parallélogrammes à une figure intermédiaire : un rectangle ayant même base et même hauteur que les deux parallélogrammes.
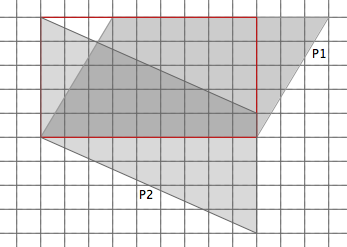
Pour cela, on peut déformer continûment le parallélogramme P1 en fixant un de ses côtés, pris comme base, et par glissement du côté opposé parallèlement à la base, le transformer en rectangle. Ensuite, on peut changer de point de vue : fixer une autre base et appliquer le même procédé pour transformer, sans en changer l’aire, le rectangle en parallélogramme P2. On peut aussi, par le même mouvement, transformer les deux figures en un même rectangle.
On peut aussi obtenir le rectangle rouge en coupant un morceau (un coin triangulaire) de P1 et en le plaçant d’un autre côté. Puis faire de même avec le parallélogramme P2.
Les deux parallélogrammes ont donc la même aire.
Une autre procédure consiste à constater que la base de P1 est la hauteur de P2 et vice versa. En évoquant la formule d’aire du parallélogramme, on conclut qu’ils ont même aire. Mais cette solution paraît assez abstraite.
Déformer un parallélogramme en gardant même aire
a) Sans utiliser les graduations de la latte (règle), déformez le parallélogramme A en un parallélogramme de même aire, tout en gardant un côté fixe.
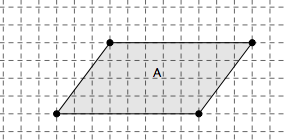
b) Même consigne en choisissant un autre côté.
Solutions
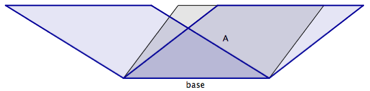
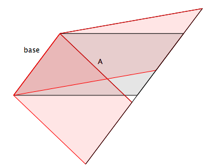
Voici quelques solutions pour transformer un parallélogramme en parallélogrammes de même aire.
Elles mettent en jeu la famille de parallélogrammes de même base et de même hauteur. Le changement de point de vue permet d’obtenir deux séries de parallélogrammes.
Déformer un parallélogramme en un rectangle
a) Sans utiliser les graduations de la latte (règle), déformez le parallélogramme B en un rectangle de même aire, tout en gardant un côté fixe.
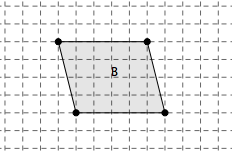
b) Même consigne en choisissant un autre côté.
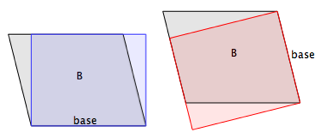
Solutions
Voici deux solutions.
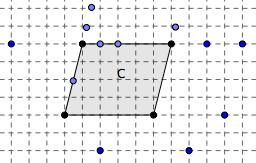
Déformer un parallélogramme en un losange
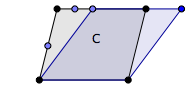
Il faut déformer le parallélogramme C en un losange de même aire, tout en gardant deux sommets fixes.
Parmi les points proposés, quels sont ceux qui pourraient être les deux autres sommets ?
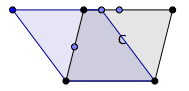
Solutions
Pour transformer un parallélogramme en losange de même aire, on peut voir celui-ci dans une famille de parallélogrammes de même base et de même hauteur.
On fait glisser un des côtés parallèlement au côté opposé jusqu’à ce que les quatre côtés aient même longueur. On peut vérifier cette égalité grâce au compas. On peut glisser vers la gauche ou vers la droite.
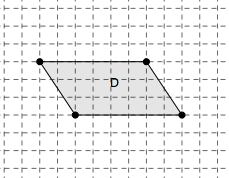
Déformer un parallélogramme en gardant même périmètre
Déformez le parallélogramme D en un parallélogramme de même périmètre, tout en gardant deux sommets fixes.
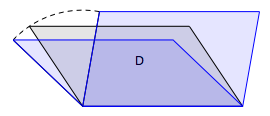
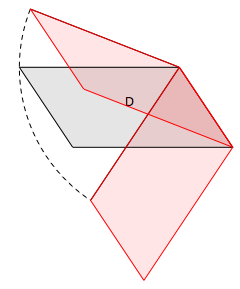
Solutions
Pour transformer un parallélogramme tout en en conservant le périmètre, on peut évoquer la famille de parallélogrammes de même base et de même périmètre. On choisit un côté comme base et on « incline » les deux côtés qui ont un sommet commun avec cette base sans en changer la longueur, à l’aide du compas. On construit ainsi toute une série de solutions. On trouve une deuxième série de parallélogrammes en changeant de point de vue.
Activités en amont
Activités en aval
Contenu visé
- Notions d’aire et de périmètre.
- Aires des parallélogrammes.
- Familles de parallélogrammes de même aire ou de même périmètre.
- Définition du losange.
- Le losange en tant que parallélogramme.
Instruments de pensée
- Mouvement et déformation de figures.
- Changement de point de vue.
- Evoquer une situation intermédiaire, la transitivité de la relation « a même aire que ».
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|