Ce que nous appelons instruments de pensée sont les démarches mentales les plus souvent utilisées pour résoudre des problèmes ou comprendre une matière.
En mathématiques, on pourrait citer des outils généraux tels que morceler un problème, envisager un cas particulier, exemplifier…
Nous nous intéressons ici aux instruments de pensée utilisés dans le cadre de la géométrie. Certains, sans être des points de matière, sont liés aux contenus auxquels ils s’appliquent, d’autres sont plus généraux et ne sont pas propres à la géométrie.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Ce texte se base en partie sur l’article suivant :
Thérèse Gilbert, Quelques instruments de pensée en géométrie,
MATH-ÉCOLE n° 193, Neufchâtel, Août 2000.
Classer ces instruments de pensée ne va pas de soi. Plusieurs classements sont possibles.
Voici quelques instruments de pensée ou classes d’instruments de pensée, que nous évoquons souvent.
1. Le changement de point de vue
2. Le mouvement
3. Créer ou disposer de liens entre différentes connaissances
4. Composer et décomposer
5. Percevoir ou s’appuyer sur la symétrie d’une situation
1. Le changement de point de vue
Une difficulté de la résolution de certains problèmes est que l’esprit reste concentré sur une façon de voir, qu’il cherche dans une direction, indiquée par un énoncé ou une figure. Une piste est alors de se forcer à voir les choses autrement, à changer de point de vue.
Par exemple, il arrive souvent que l’on doive redresser mentalement une figure pour l’amener dans une position privilégiée où les directions horizontale et verticale permettent d’autres visions, d’autres intuitions, d’autres pistes de recherches.
Illustrons cet outil par une activité.
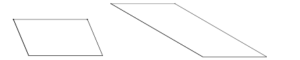
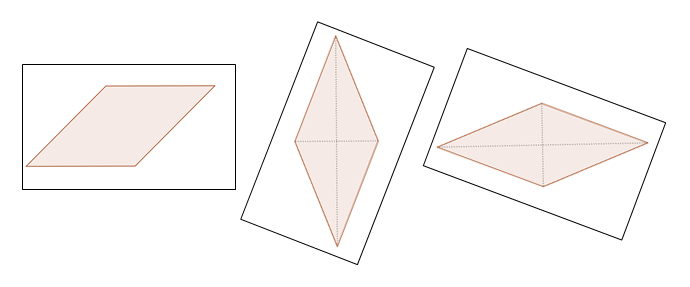
Énoncé. Découpez en deux morceaux chacun de ces parallélogrammes, puis assemblez les deux morceaux pour construire chaque fois un rectangle. 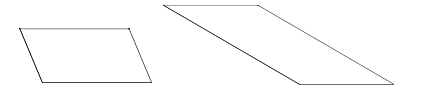 Solution. Une méthode envisageable est de couper suivant un seul trait vertical. Pour la première figure, voici une solution parmi d’autres.  Pour la deuxième, un seul trait vertical ne suffit pas. Plusieurs coups de ciseaux verticaux et horizontaux permettent de trouver une solution pour construire un rectangle, mais le nombre de morceaux est plus élevé. 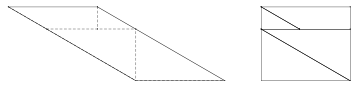 Par contre, on peut prendre un côté oblique comme « base » de découpage et découper selon un trait perpendiculaire à cette base en ne faisant que deux morceaux. Cela revient à faire pivoter mentalement le parallélogramme pour amener la base choisie en position horizontale. Voilà ce que nous appelons changer de point de vue. 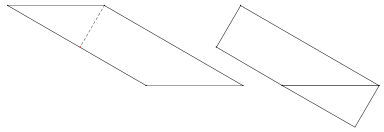 |
Il arrive aussi qu’il faille focaliser son attention sur autre chose que ce que l’on distingue dans un premier temps. Par exemple, un assemblage de deux segments de même longueur peuvent devenir avantageusement les côtés d’un triangle isocèle ou deux rayons d’un même cercle…
Remarquons que pour changer de point de vue, on peut souvent utiliser un autre instrument de pensée qu’est le mouvement pensé.
Des activités et des démonstrations où le changement de point de vue est utilisé :
Activité sur l’aire des parallélogrammes à 10-12 ans.
Activité de comparaison et déformation de figures à 10-12 ans.
Activité sur l’aire des triangles à 12-14 ans.
Une démonstration du théorème de Thalès par les aires de parallélogrammes à 14-15 ans.
Vers une démonstration du théorème de Thalès par les aires de triangles à 14-15 ans.
Une démonstration du théorème de Thalès par les aires de triangles à 14-15 ans.
2. Le mouvement
La possibilité d’imaginer des mouvements prend une place importante dans la pensée géométrique en recherche. L’idée de mouvement intervient de plusieurs façons.
Le mouvement est utilisé pour amener une figure dans une position privilégiée, pour changer de point de vue. Certaines figures sont plus facilement identifiables dans une position privilégiée. Par exemple, on reconnaît plus facilement un losange lorsque une de ses diagonales est verticale. Dans cette position, la symétrie de la figure apparaît clairement. Pour amener une figure dans la position qui provoquera le plus d’intuitions, qui permettra d’établir le plus facilement des liens avec d’autres figures, qui mettra en évidence ses propriétés, il n’est pas toujours nécessaire ni possible de la redresser effectivement. Il suffit souvent de « penser ce mouvement » de redressement. Remarquons que les étapes intermédiaires du mouvement ont dans ce cas peu d’importance, l’essentiel étant d’imaginer la figure en position privilégiée.
| Pour décider si la figure suivante est un losange, il peut être bien utile de « tourner la tête » (ou sa feuille). |
Pour lire un plan de ville, il est aussi utile, quoique non nécessaire, de pouvoir le faire tourner mentalement. Il en va de même pour déterminer la droite et la gauche d’une personne qui se trouve en face de nous ou pour imaginer la vue qu’elle a d’un objet qui nous apparaît sous un autre point de vue. Le « mouvement pensé » constitue donc aussi un moyen d’appréhender l’espace.
Le mouvement engendre des figures géométriques. Le cercle est engendré par une extrémité d’un segment qui tourne autour de l’autre. Le troisième sommet d’un triangle isocèle dont la « base » est fixée peut engendrer la médiatrice du segment pris comme base. Les surfaces de révolution telles la sphère, le cylindre ou le cône
sont engendrées par la rotation d’une courbe (cercle, droite…) autour d’un axe. Le fait de les voir ainsi au lieu de les considérer seulement comme des ensembles de points vérifiant une propriété (d’équidistance par exemple) est source d’autres intuitions utiles.
Comment déplacer le point C pour que le triangle ABC reste isocèle ?
Les solutions possibles forment la médiatrice du segment [AB]. (Cliquer sur le point C pour voir les solutions.)
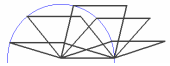
Le mouvement est utilisé pour parcourir une famille infinie d’objets et accéder à des objets extrêmes. On l’évoque, par exemple, pour parcourir tous les losanges dont un côté est donné.
L’avantage du mouvement est de procurer au passage ou aux extrémités les figures ou des situations particulièrement intéressantes.
Dans l’exemple donné, le losange se transforme au passage en carré. Par contre, pour voir que ces losanges n’ont pas tous la même aire, on peut par exemple considérer le cas extrême où les quatre sommets sont alignés et où l’aire est nulle.

Le mouvement crée ainsi des liens entre notions géométriques. C’est le cas ci-dessus pour le losange et le carré. Quatre tiges articulées fournissent un moyen de visualiser le mouvement permettant de passer d’une figure à l’autre.
Des activités et des démonstrations où le mouvement est utilisé :
Activité sur des familles de parallélogrammes à 10-12 ans.
Activité de comparaison et déformation de figures à 10-12 ans.
Activité sur l’aire des triangles à 10-12 ans.
Activité sur l’aire des triangles à 12-13 ans.
Activité sur des familles de parallélogrammes à 12-13 ans.
Quelques formules d’aire à 10-12 ans
Une démonstration du théorème de Thalès par les aires de parallélogrammes à 14-15 ans.
Vers une démonstration du théorème de Thalès par les aires de triangles à 14-15 ans.
Une démonstration du théorème de Thalès par les aires de triangles à 14-15 ans.
3. Créer ou disposer de liens entre connaissances
Face à un problème de mathématiques, il faut souvent « penser à côté », rattacher la situation à d’autres plus connues. Dans le cas d’un problème géométrique, il s’agit parfois de compléter une figure, de l’enrichir, d’imaginer des lignes supplémentaires faisant apparaître de nouvelles figures ou au contraire d’appauvrir une situation, d’en isoler une partie par la pensée pour ne plus y voir qu’une figure clé, source d’intuition.
Voir l’invisible. On enrichit une figure pour y voir des figures sources d’intuition ou de connaissances. Lors de la résolution d’un problème géométrique, pour pouvoir appliquer ses connaissances, il faut souvent pouvoir repérer des figures familières. Pour cela il est parfois nécessaire de compléter la situation donnée par exemple en y traçant de nouveaux segments.
Illustrons cette méthode par une activité.
Énoncé. Le rectangle ci-dessous est-il inscriptible dans un cercle ?  Solution. Pour le voir, munissons ce rectangle de ses diagonales. Comme elles sont de même longueur et se coupent en leur milieu, les quatre sommets sont à égale distance de leur intersection O. Ils sont donc sur un cercle de centre O. |
D’une façon générale, pour pouvoir évoquer les situations utiles à la résolution d’un problème et y voir l’invisible, il est essentiel de s’être forgé des images mentales et d’avoir vécu des activités qui permettent de les faire ressurgir au moment opportun, c’est-à-dire qui facilitent le transfert des connaissances.
Évoquer une situation intermédiaire. Lorsque l’on doit comparer deux situations (par exemple, montrer une égalité, une isométrie, ou une inégalité), il arrive souvent que l’on soit amené à comparer les deux situations à une troisième, qu’il faut donc éventuellement créer.
On peut en trouver un exemple dans Comparaison et déformation de figures (première activité).
Pour créer de telles situations intermédiaires, il est nécessaire de disposer de suffisamment d’images mentales et de relations entre les concepts et les figures.
Isoler par la pensée. Il arrive souvent que des éléments d’un problème doivent être momentanément mis entre parenthèses pour concentrer son attention sur la partie sur laquelle peuvent être appliquées différentes connaissances.
On peut en trouver des exemples dans Comparaison et déformation de figures (deuxième activité, construction du losange) et dans Aires de parallélogrammes (consigne c).
Des activités et des démonstrations où l’on crée des liens, où on en évoque ou bien où il faut isoler par la pensée: cet instrument de pensée, vaste, est tellement souvent utilisé que nous pourrions citer toutes les activités géométriques…
Activité de comparaison et déformation de figures à 10-12 ans.
Quelques formules d’aire à 10-12 ans.
Activités sur des familles de parallélogrammes à 10-12 ans.
Activités de dissections géométriques à 10-12 ans.
Activités sur des familles de parallélogrammes à 12-13 ans.
Activité sur l’aire des triangles à 12-13 ans.
Une démonstration du théorème de Thalès par les aires de parallélogrammes à 14-15 ans.
Vers une démonstration du théorème de Thalès par les aires de triangles à 14-15 ans.
Une démonstration du théorème de Thalès par les aires par les aires de triangles à 14-15 ans.
4. Composer et décomposer
Dans les problèmes d’aire par exemple, il est souvent utile de décomposer une figure en plusieurs autres et éventuellement de les assembler autrement comme les pièces d’un puzzle pour retrouver une figure connue. Par exemple, l’aire d’un trapèze égale celle d’un certain parallélogramme.
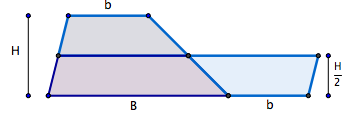
C’est une pratique courante pour établir ou retrouver certaines formules d’aire de quadrilatères. Cet outil est aussi utilisé pour établir certaines égalités d’aire comme dans la preuve du théorème de Pythagore illustrée ci-dessous.
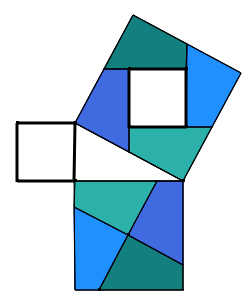
On peut aussi décomposer et recomposer dans d’autres types de problèmes. Par exemple, pour obtenir le périmètre de la figure suivante, on peut déplacer certains segments pour constituer une figure dont le périmètre peut être saisi plus facilement.
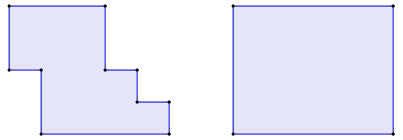
Des activités et des démonstrations où l’on est amenés à composer ou décomposer:
Activité de comparaison et déformation de figures à 10-12 ans.
Quelques formules d’aire à 10-12 ans.
Activités de dissections géométriques à 10-12 ans.
Activités sur des familles de parallélogrammes à 12-13 ans.
Activité sur l’aire des triangles à 12-13 ans.
5. Percevoir ou s’appuyer sur la symétrie d’une situation
La symétrie joue un grand rôle dans nos perceptions. Par exemple, on voit mieux si un parallélogramme particulier est un losange en repérant son éventuel axe de symétrie, encore plus visible si on l’amène en position verticale.
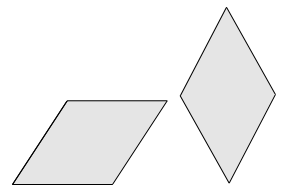
De plus certaines de nos intuitions sont fondées sur la symétrie. Par exemple, on se persuade aisément que tout triangle ayant deux côtés de même longueur a deux angles de même amplitude en évoquant la symétrie de la figure.
Mais la symétrie peut aussi intervenir comme argument dans la résolution de problème.
Énoncé. Tracez le ou les triangle(s) de base [AB] et dont les deux autres côtés sont le longueur 4 cm et 5 cm.  Solutions. Dès qu’on a un triangle, par symétrie, on sait que l’on aura trois autres triangles, superposables au premier. En effet, si on a situé le point C au-dessus de [AB], plus près de B, on sait qu’une construction symétrique, plaçant C plus près de A, est possible. De même, toutes les constructions peuvent être faites en dessous de [AB]. Solutions. Dès qu’on a un triangle, par symétrie, on sait que l’on aura trois autres triangles, superposables au premier. En effet, si on a situé le point C au-dessus de [AB], plus près de B, on sait qu’une construction symétrique, plaçant C plus près de A, est possible. De même, toutes les constructions peuvent être faites en dessous de [AB]. 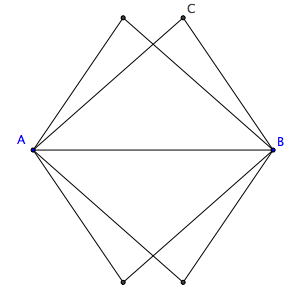 L’ensemble des solutions possède deux axes de symétrie : la droite AB et la médiatrice de [AB]. L’ensemble des solutions possède deux axes de symétrie : la droite AB et la médiatrice de [AB]. |
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|