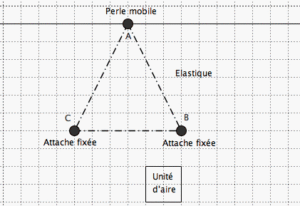
Les activités suivantes proposent de comparer des triangles de deux familles notamment selon leur aire et leur périmètre. Elles peuvent être un point de départ pour établir la formule d’aire du triangle.
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
Deux familles de triangles : découverte

Matériel : chaque groupe dispose de deux types de matériel (voir photo ci-dessous). Ce matériel est schématisé par les figures qui suivent.
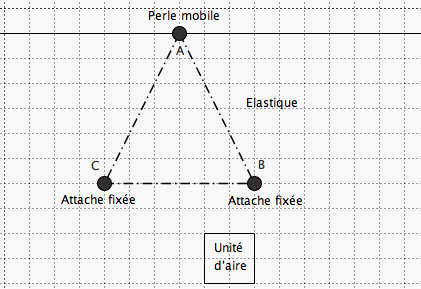
Le premier matériel est constitué d’un élastique tendu passant par deux attaches parisiennes fixées (B et C) et par une perle (A) qui peut coulisser sur une pique à brochette fixée. Cette dernière est parallèle
à BC.
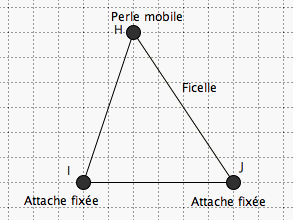
Le deuxième est constitué d’une ficelle tendue passant par deux
attaches parisiennes fixes (I et J) et sur laquelle est enfilée une perle mobile (H).
Dans chaque cas, on a glissé du papier quadrillé sur lequel on peut dessiner.
Comparez librement les triangles que l’on peut obtenir dans chaque cas.
Solutions
Cette activité de constatation libre permet à l’enseignant de voir ou de revoir beaucoup
de notions telles que les caractéristiques des triangles liées aux angles ou aux côtés,
l’aire des triangles, leur périmètre, leur hauteur.
Deux familles de triangles : aire et périmètre
1. a) Placez la perle de la première maquette en A. Tracez un parallélogramme ou un rectangle qui vous permet de calculer l’aire du triangle ABC. Quelle est-elle ?
b) Déplacez la perle. Comment varient l’aire et le périmètre du triangle ?
2. a) Avec la deuxième maquette, comment obtenir le triangle de périmètre le plus petit ? Le plus grand ?
b) L’aire du triangle varie-t-elle ?
Solutions
1. a) Si les élèves n’ont pas vu la formule d’aire du triangle, cette activité permet de l’établir. On peut dessiner un rectangle ou un parallélogramme d’aire double de celle du triangle. On peut compter le nombre de carrés unités et le diviser par deux, ou bien se baser sur la formule d’aire du parallélogramme et en profiter pour en déduire celle du triangle.
b) Comme la pique à brochette est parallèle à la base du triangle, tous les triangles ainsi représentés ont la même aire.
Par ailleurs, plus on éloigne la perle du point A, plus le périmètre augmente. On se contente ici de l’expérimenter en tirant sur l’élastique.
On rencontre ici des triangles de même aire mais de périmètres très différents.
Cette activité mène ainsi à la proposition suivante :
– si deux triangles ont la même base et les sommets opposés à cette base sur une droite parallèle à celle-ci, alors ils ont la même aire.
Question de relance
Le mouvement physique de la perle, prolongé par un mouvement mental, permet de parcourir cette famille de triangles.
On peut imaginer des triangles très « étirés » mais ayant tous la même aire que
le triangle initial ABC, ce qui ne va pas de soi.
Et si on incline un peu la pique, comment
varie l’aire des triangles que l’on obtient ?
2. a) La deuxième maquette présente une famille de triangles de même périmètre.
C’est la notion même de périmètre que l’on travaille donc ici.
b) Le fait que l’aire varie peut être comprise par l’examen de deux cas extrêmes,
lorsque la perle (H)
est presque alignée avec les deux attaches (I et J) vers la gauche ou la droite.
Le fait qu’elle soit maximale pour le triangle isocèle (de base [IJ])
peut être simplement constaté.
Activités en amont
Représentations et déformations de triangles
Activités en aval
Aires de triangles à 10 -12 ans
Trois formes de la formule d’aire des triangles
Dissections géométriques à 10 – 12 ans
Familles de triangles à 12 – 14 ans
Instruments de pensée
Mouvement, famille et déformation de figures
Créer des liens entre des figures.
Contenu visé
Familles de triangles
Aire de triangles (voir aussi Formules d’aire de quelques figures planes)
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |