Cette synthèse porte sur deux familles de triangles qui ont leur base constante et leur hauteur qui varie ou non.
Par la suite, on rappelle les trois formes de la formule d’aire du triangle
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
1. Famille de triangles qui ont tous la même base
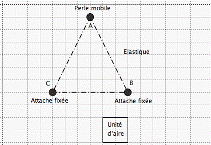
Triangles de même aire
– Lorsqu’on déplace le troisième sommet d’un triangle sur une droite parallèle à la base, l’aire du triangle ne change pas.
Dès lors, si deux triangles ont la même base et si les troisièmes sommets de chacun des triangles se trouvent sur une droite parallèle à la base, ils ont la même aire
– Le périmètre de ces triangles varie.
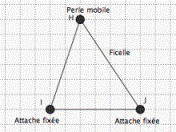
Triangles de même périmètre
– Lorsqu’on déplace le troisième sommet (la base est fixe) de telle sorte que le périmètre reste identique, on constate qu’un côté s’allonge tandis que l’autre diminue d’autant.
– La hauteur du triangle varie.
– L’aire du triangle varie.
2. Trois formules pour calculer l’aire du triangle
Aire du triangle :
![]() ou
ou ![]()
Aire du triangle :
![]() ou
ou ![]()
Aire du triangle :
![]() ou
ou ![]()
Remarque :
Si cette présentation sous forme de fraction est courante chez les enseignants, il nous semble nécessaire de d’abord présenter ces formules en utilisant le signe « : » ==> ( B x h ) : 2, ( B : 2 ) x h , B x ( h : 2) .
Le passage de « : 2 » à « ![]() » est loin d’être évident. Pour certains élèves, «
» est loin d’être évident. Pour certains élèves, « ![]() » n’évoque que l’idée de « demi ».
» n’évoque que l’idée de « demi ».
Activités liées à ce contenu
Représentations et déformations de triangles
Trois formes de la formule d’aire des triangles
Instruments de pensée
Mouvement, famille et déformation de figures
Faire des liens entre figures
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |

