L’activité en bref
L’objectif est de déterminer les probabilités d’obtenir les sommes 9 et 10 en lançant trois dés. [1]Cet énoncé est connu comme « problème de Galilée » ou comme « paradoxe du prince de Toscane».
Public cible
Toutes classes ayant dans leur programme l’étude des probabilités : 6GT, 6TT, 6TQ et 7ème.
Toutes classes ayant étudié la boite à moustache : 4GT et 4TT
Enjeux
- Adopter une démarche expérimentale.
- Aborder les notions d’expérience aléatoire et d’événements.
- Traiter des données et illustrer les résultats avec la boite à moustaches.
- Comprendre le lien entre fréquences et probabilités.
- Déterminer des probabilités à partir de combinaisons.
- Appréhender la fluctuation d’échantillonnage en lien avec la taille de l’échantillon.
Matériel
Trois dés par élève.
Fichier Excel des simulations (voir l’annexe de ce document).
Durée
Environ 2 heures de cours (3h si les élèves réalisent les boites à moustaches à la main).
Énoncé
Le prince de Toscane demanda un jour à Galilée : pourquoi lorsqu’on jette trois dés, obtient-on plus souvent la somme 10 que la somme 9, bien que ces deux sommes soient obtenues chacune de six façons différentes ?
L’observation du prince de Toscane est-elle vraie ? Et si oui, pourquoi ?
Étape 1 : Expérimentation
Lancez 20 fois 3 dés et notez combien de fois vous avez obtenu 9 et combien de fois vous avez obtenu 10 (nous supposons que tous les dés sont parfaitement équilibrés).
| Obtenir 9 | Obtenir 10 | Autres sommes | Total des lancers |
| 20 |
Donnez les 6 façons d’obtenir 9 et les 6 façons d’obtenir 10 en lançant 3 dés.
| Obtenir 9 | Obtenir 10 |
Quelle somme avez-vous eu le plus ?
Est-ce que cela est suffisant pour confirmer ou infirmer les propos du prince de Toscane ?
Que pourrions-nous faire pour confirmer ou infirmer ?
Étape 2 : Relevé des résultats de toute la classe :
| Elève | Obtenir 9 | Obtenir 10 | Total des lancers |
| 1 | 20 | ||
| 2 | |||
| 3 | |||
| … | |||
| 24 | |||
| 25 | |||
| Total : | |||
| Fréquence : |
Peut-on à présent émettre une hypothèse sur les fréquences d’obtenir 9 et 10?
Étape 3 : Simulations
Voici les résultats d’une simulation effectuant 10 000 lancers de triplets de dés :
Nombre de fois que j’ai obtenu une somme égale à 3: 45
Nombre de fois que j’ai obtenu une somme égale à 4: 158
Nombre de fois que j’ai obtenu une somme égale à 5: 243
Nombre de fois que j’ai obtenu une somme égale à 6: 495
Nombre de fois que j’ai obtenu une somme égale à 7: 672
Nombre de fois que j’ai obtenu une somme égale à 8: 946
Nombre de fois que j’ai obtenu une somme égale à 9: 1149
Nombre de fois que j’ai obtenu une somme égale à 10: 1253
Nombre de fois que j’ai obtenu une somme égale à 11: 1268
Nombre de fois que j’ai obtenu une somme égale à 12: 1168
Nombre de fois que j’ai obtenu une somme égale à 13: 965
Nombre de fois que j’ai obtenu une somme égale à 14: 666
Nombre de fois que j’ai obtenu une somme égale à 15: 507
Nombre de fois que j’ai obtenu une somme égale à 16: 292
Nombre de fois que j’ai obtenu une somme égale à 17: 128
Nombre de fois que j’ai obtenu une somme égale à 18: 45
Déterminez les fréquences d’obtention des sommes 9 et 10 :
D’après la simulation, le prince de Toscane avait-il raison?
Cependant, pouvons-nous faire confiance à cette simulation ? L’écart entre les fréquences de 9 et 10 est-il réel ou uniquement dû au hasard? Pour régler ce problème, il suffit de répéter la simulation plusieurs fois pour observer si il y a réellement une différence entre ces deux fréquences.
Étape 4 : Comparaison des simulations
On a réalisé 80 simulations de :
- 10 lancers de trois dés
- 100 lancers de trois dés
- 1000 lancers de trois dés
- 10000 lancers de trois dés
Pour chaque simulation on a calculé uniquement les fréquences d’observation des sommes égales à 9 et à 10. En annexe, vous trouverez les différentes fréquences à l’issue des simulations (en écriture décimale et en pourcentage) dans le fichier Excel ci-joint .[2]Pour les personnes intéressées vous trouverez en annexe le code python qui a permis de réaliser ces simulations
Comparer les résultats des 4 types de simulations (10, 100, 1000 et 10000 lancers), en dessinant les boites à moustaches des fréquences d’obtention de 9 et 10 pour chacune des simulations.
La simulation réalisée précédemment à l’étape 3 peut-elle être considérée comme fiable ?
A partir de combien de lancers des trois dés peut-on considérer qu’une simulation est fiable ?
Étape 5 : Approche théorique
Nous avons constaté que l’expérimentation ne nous permet pas de conclure sur la question du prince de Toscane à partir des fréquences d’observation de 9 et 10. Cependant, les simulations montrent une plus grande fréquence de la somme égale à 10 par rapport à celle égale à 9 lorsque le nombre de lancers devient très grand (au-delà de 1000, la largeur des boites à moustaches devient suffisamment petite pour observer une différence dans les fréquences de « 9 » et de « 10 »).
Comment peux-tu expliquer cette prévision sur base de la symétrie des dés ?
Éléments de réponses et quelques commentaires didactiques
Étape 1 :
Cette étape permet aux élèves de réfléchir aux combinaisons possibles d’obtenir 9 ou 10 avec trois nombres naturels inférieurs ou égaux à 6.
A ce stade, il est fort probable que les élèves observent des résultats très différents (certains ayant plus de 9 que de 10 et d’autres inversement). Il n’est donc pas possible de tirer une conclusion.
Étape 2 :
Deux cas de figures peuvent se produire :
- Les fréquences de 9 et 10 sont proches.
- Les fréquences de 9 et 10 sont relativement éloignées.
Quelle que soit la situation, même si la classe contient 30 élèves, il est risqué de conclure à ce stade qu’une somme est plus fréquente que l’autre.
Étape 4 :
Comme il y a un grand nombre de boites à réaliser, il est conseillé de les dessiner à l’aide de Géogebra.
Méthode pour réaliser les boites :
- Ouvrir Geogébra et aller dans l’onglet « affichage » et sélectionner « Tableur ».
- Dans le tableur qui vient de s’ouvrir, copier-coller les données du tableau en annexe ou du fichier Excel reprenant les résultats de 80 simulations avec un nombre de lancers déterminé.
- Vous allez réaliser une boite à moustache par colonne (Voir en annexe la vidéo explicative):
- Dans la barre d’insertion de valeurs, sélectionner le type de Boite à moustaches suivant : BoiteMoustache(<Ordonnée>,<demi-hauteur>,<série brute>)
- Dans ordonnée sélectionner un entier différent pour chaque boîte et ayant un écart de plus de deux fois la demi-hauteur. Exemple 0, 5, 10, 15,… si demi-hauteur = 2.
- Pour « série brute », sélectionnez l’intervalle correspondant à vos données. Nous vous conseillons de prendre les fréquences exprimées en pourcentage pour mieux observer les boites.
- Penser à nommer votre boite. Pour ce faire, sélectionner votre boite dans la partie algèbre et aller dans propriétés. Une fenêtre s’ouvrira à droite, aller dans l’option basique pour changer de nom. Exemple : FréqDe9sur10lancers (Attention, il faut tout mettre en un mot).
- Voici une illustration de plusieurs boites réalisées pour l’activité:
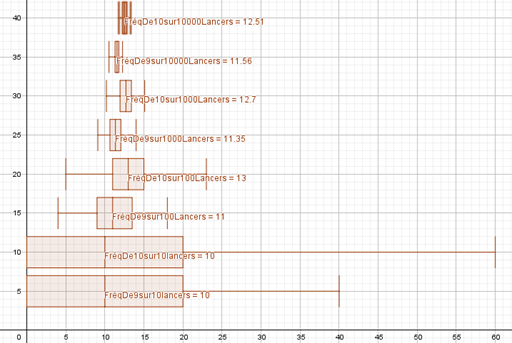
Figure 1 : boite à moustaches des résultats 9 et 10 sur 80 simulations pour 10, 100, 1000 et 10000 lancers [3]Données en pourcentage
Interprétation des résultats :
On constate que les médianes sont à chaque fois indiquées et que pour 10 000 lancers, les fréquences obtenues par la simulation donnée à l’étape 3 sont proches de la médiane obtenue à partir des 80 simulations de 10 000 lancers. En effet, « Obtenir 9 » a comme médiane 11,56 (11,49 pour la simulation étape 3) et « Obtenir 10 » a comme médiane 12,53 (12,53 pour la simulation étape 3).
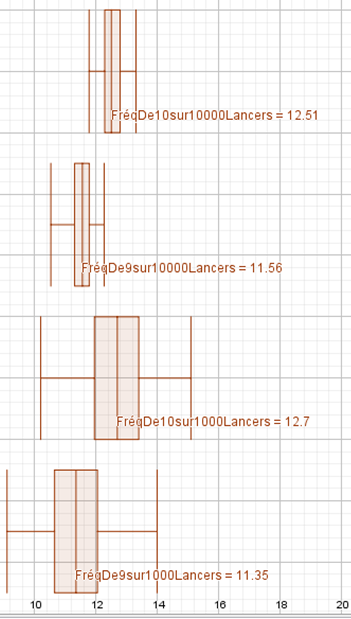
Figure 2 : zoom : boite à moustaches des résultats 9 et 10 pour 80 simulations de 1000 et 10000 lancers.[4]Données en pourcentage
En regardant les boites, nous constatons qu’à partir de 1000 lancers la différence de position des boites « obtenir 9 » et « obtenir 10 » devient observable (les 50% de données centrales ne se superposant plus). Avec moins de 1000 lancers, il est difficile de déterminer si l’écart de position entre les boites est dû à la variabilité des données des simulations ou si il y a un écart entre les probabilités d’obtenir « 9 » et d’obtenir « 10 ».
Etape 5 :
Explications : Si nous supposons que les trois dés sont parfaitement symétriques et que toutes les faces ont les mêmes chances d’apparaître, les issues possibles pour la somme vont de 3 à 18. Mais, on se rend vite compte que certaines sommes ont plus de chances que d’autres d’apparaître. 3, par exemple ne peut être obtenu qu’en ayant 1+1+1.
Pour 9, par contre, on peut avoir 1+2+6, 1+3+5, 1+4+4, 2+2+5, 2+3+4, 3+3+3.
Pour 10, on peut avoir 1+3+6, 1+4+5, 2+2+6, 2+3+5, 2+4+4, 3+3+4.
Pour 9 et 10, on a le même nombre de décompositions additives mais en regardant de plus près on se rend compte que la somme 3+3+3, par exemple, est plus rare que la somme 2+3+5; la première ne s’obtient que d’une seule manière mais la seconde peut s’obtenir de 6 façons différentes car les trois dés sont distincts : 2+3+5, 2+5+3, 3+5+2, 3+2+5, 5+2+3, 5+3+2. Faisons le décompte total. Pour le premier dé, il y a six possibilités. Pour chaque possibilité du premier dé, il y a six possibilités pour le second, ce qui fait 36 en tout. Pour chacune des possibilités des deux premiers dés, il y en a six pour le troisième, ce qui fait 216 au total. Comptabilisons alors les possibilités de chaque somme (voir le tableau ci-dessous).
| Obtenir 9 | Obtenir 10 | ||
| Somme | Combinaisons | Somme | Combinaisons |
| 1+2+6 | 6 | 1+3+6 | 6 |
| 1+3+5 | 6 | 1+4+5 | 6 |
| 1+4+4 | 3 | 2+2+6 | 3 |
| 2+2+5 | 3 | 2+3+5 | 6 |
| 2+3+4 | 6 | 2+4+4 | 3 |
| 3+3+3 | 1 | 1+3+6 | 6 |
| Total : | 25 | Total : | 27 |
On en conclut que la probabilité d’avoir une somme égale à 9 vaut 25/216 (soit environ 0,1157) tandis que la probabilité que la somme soit égale à 10 vaut 27/216 (soit 0,125).
La différence des probabilités de ces deux évènements est donc très faible. On peut donc se demander si les propos du prince de Toscane sont réalistes. Une personne est-elle capable d’observer de son vivant un écart aussi faible?
Quelques échos des classes
L’activité telle quelle n’a jamais été testée mais une première version a été testée dans trois classes (deux de 6TQ et une de 7PC).
Le sel du problème
Cette activité permet de faire le lien entre fréquences et probabilités (dans le programme de 6ème secondaire) avec une expérience dont les élèves ne connaissent pas à l’avance les résultats mais dont on peut vérifier ceux-ci à la fin de l’activité. Les approches « fréquentiste et classique » par les combinaisons sont visées[5]Nous reprenons ces termes à Batanero C., Chernoff E.J., Engel J., Lee H.S., Sánchez E. (2016) Research on Teaching and Learning Probability. In: Research on Teaching and Learning Probability. … Continue reading. Pour l’approche “classique” ,d’autres parlent de probabilité théorique ou de probabilité à priori. Tandis que pour l’approche fréquentiste, certains parlent de probabilité à postériori.
Annexe
1) Lien vidéo tutoriel : https://www.youtube.com/watch?v=jUAZbVoeXD8
2) Le pdf de l’activité:
3) Le fichier excel:
4) Code python:
import random # importation du module de création de nombre aléatoire
Nbr_Lancer = int(input(« combien de lancers par simulation? »))
nbr_simulation=int(input(« combien de simulations? »))
Somme1=int(input(« Veillez donner la première somme des trois dés que vous souhaitez étudier »))
Somme2=int(input(« Veillez donner la deuxième somme des trois dés que vous souhaitez étudier »))
def resultatSomme3Des ():
Des1 = random.randint(1, 6)
Des2 = random.randint(1, 6)
Des3 = random.randint(1, 6)
Somme = Des1 + Des2 + Des3
return Somme
def obtenirSomme3Des(NombreSouhaite1, NombreSouhaite2):
Resultat = 0
Compteur1=0
Compteur2=0
if NombreSouhaite1 == NombreSouhaite2:
print(« le deux nombres doivent être différent »)
else:
for j in range (Nbr_Lancer): #par simulation je fais tout mes lancés
#Je lance à chaque fois trois dés dont j’additionne les valeurs
Resultat = resultatSomme3Des ()
if Resultat ==NombreSouhaite1:#je compte combien de fois j’obtiens la première somme voulue
Compteur1 = Compteur1 + 1
if Resultat ==NombreSouhaite2:#je compte combien de fois j’obtiens la première somme voulue
Compteur2 = Compteur2 + 1
print (Compteur1/Nbr_Lancer,’;’,end = ‘ ‘)
print (Compteur2/Nbr_Lancer)
#à chaque simulation j’imprime la fréquence d’avoir obtenu la somme en question.
#Les impressions se font les unes à coté des autres pour obtenir un fichier utilisable par excel
for i in range (nbr_simulation):
obtenirSomme3Des(Somme1,Somme2)
80 simulations de 10 lancers :
| 10 lancers | |||
| fréquences | pourcentage | ||
| Obt9 | Obt10 | Obt9 | Obt10 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,1 | 0,1 | 10 | 10 |
| 0,2 | 0,1 | 20 | 10 |
| 0,2 | 0,1 | 20 | 10 |
| 0,2 | 0,1 | 20 | 10 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,2 | 0,2 | 20 | 20 |
| 0,3 | 0,2 | 30 | 20 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,3 | 30 | 30 |
| 0,3 | 0,4 | 30 | 40 |
| 0,3 | 0,5 | 30 | 50 |
| 0,4 | 0,6 | 40 | 60 |
80 simulations de 100 lancers :
| 100 lancers | |||
| fréquences | % | ||
| Obt9 | Obt10 | Obt9 | Obt10 |
| 0,04 | 0,05 | 4 | 5 |
| 0,06 | 0,06 | 6 | 6 |
| 0,06 | 0,07 | 6 | 7 |
| 0,06 | 0,07 | 6 | 7 |
| 0,06 | 0,08 | 6 | 8 |
| 0,06 | 0,08 | 6 | 8 |
| 0,07 | 0,08 | 7 | 8 |
| 0,07 | 0,08 | 7 | 8 |
| 0,07 | 0,08 | 7 | 8 |
| 0,08 | 0,09 | 8 | 9 |
| 0,08 | 0,09 | 8 | 9 |
| 0,08 | 0,09 | 8 | 9 |
| 0,08 | 0,09 | 8 | 9 |
| 0,08 | 0,1 | 8 | 10 |
| 0,08 | 0,1 | 8 | 10 |
| 0,09 | 0,1 | 9 | 10 |
| 0,09 | 0,1 | 9 | 10 |
| 0,09 | 0,1 | 9 | 10 |
| 0,09 | 0,1 | 9 | 10 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,09 | 0,11 | 9 | 11 |
| 0,1 | 0,11 | 10 | 11 |
| 0,1 | 0,12 | 10 | 12 |
| 0,1 | 0,12 | 10 | 12 |
| 0,1 | 0,12 | 10 | 12 |
| 0,1 | 0,12 | 10 | 12 |
| 0,1 | 0,12 | 10 | 12 |
| 0,11 | 0,12 | 11 | 12 |
| 0,11 | 0,12 | 11 | 12 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,11 | 0,13 | 11 | 13 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,12 | 0,14 | 12 | 14 |
| 0,13 | 0,14 | 13 | 14 |
| 0,13 | 0,14 | 13 | 14 |
| 0,13 | 0,14 | 13 | 14 |
| 0,13 | 0,15 | 13 | 15 |
| 0,13 | 0,15 | 13 | 15 |
| 0,13 | 0,15 | 13 | 15 |
| 0,14 | 0,15 | 14 | 15 |
| 0,14 | 0,15 | 14 | 15 |
| 0,14 | 0,15 | 14 | 15 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,16 | 14 | 16 |
| 0,14 | 0,17 | 14 | 17 |
| 0,15 | 0,17 | 15 | 17 |
| 0,15 | 0,17 | 15 | 17 |
| 0,15 | 0,17 | 15 | 17 |
| 0,15 | 0,18 | 15 | 18 |
| 0,15 | 0,18 | 15 | 18 |
| 0,15 | 0,18 | 15 | 18 |
| 0,16 | 0,18 | 16 | 18 |
| 0,17 | 0,18 | 17 | 18 |
| 0,17 | 0,2 | 17 | 20 |
| 0,18 | 0,23 | 18 | 23 |
80 simulations de 1000 lancers :
| 1000 lancers | |||
| fréquences | % | ||
| Obt9 | Obt10 | Obt9 | Obt10 |
| 0,091 | 0,102 | 9,1 | 10,2 |
| 0,093 | 0,108 | 9,3 | 10,8 |
| 0,093 | 0,109 | 9,3 | 10,9 |
| 0,094 | 0,11 | 9,4 | 11 |
| 0,097 | 0,112 | 9,7 | 11,2 |
| 0,098 | 0,112 | 9,8 | 11,2 |
| 0,1 | 0,112 | 10 | 11,2 |
| 0,101 | 0,114 | 10,1 | 11,4 |
| 0,101 | 0,114 | 10,1 | 11,4 |
| 0,101 | 0,114 | 10,1 | 11,4 |
| 0,101 | 0,116 | 10,1 | 11,6 |
| 0,102 | 0,116 | 10,2 | 11,6 |
| 0,104 | 0,116 | 10,4 | 11,6 |
| 0,104 | 0,117 | 10,4 | 11,7 |
| 0,105 | 0,117 | 10,5 | 11,7 |
| 0,105 | 0,117 | 10,5 | 11,7 |
| 0,105 | 0,118 | 10,5 | 11,8 |
| 0,106 | 0,118 | 10,6 | 11,8 |
| 0,106 | 0,119 | 10,6 | 11,9 |
| 0,106 | 0,119 | 10,6 | 11,9 |
| 0,107 | 0,12 | 10,7 | 12 |
| 0,107 | 0,121 | 10,7 | 12,1 |
| 0,107 | 0,121 | 10,7 | 12,1 |
| 0,108 | 0,121 | 10,8 | 12,1 |
| 0,109 | 0,121 | 10,9 | 12,1 |
| 0,109 | 0,122 | 10,9 | 12,2 |
| 0,109 | 0,122 | 10,9 | 12,2 |
| 0,109 | 0,122 | 10,9 | 12,2 |
| 0,11 | 0,122 | 11 | 12,2 |
| 0,11 | 0,122 | 11 | 12,2 |
| 0,11 | 0,123 | 11 | 12,3 |
| 0,11 | 0,123 | 11 | 12,3 |
| 0,111 | 0,123 | 11,1 | 12,3 |
| 0,112 | 0,124 | 11,2 | 12,4 |
| 0,112 | 0,125 | 11,2 | 12,5 |
| 0,112 | 0,125 | 11,2 | 12,5 |
| 0,112 | 0,125 | 11,2 | 12,5 |
| 0,112 | 0,125 | 11,2 | 12,5 |
| 0,113 | 0,126 | 11,3 | 12,6 |
| 0,113 | 0,127 | 11,3 | 12,7 |
| 0,114 | 0,127 | 11,4 | 12,7 |
| 0,114 | 0,127 | 11,4 | 12,7 |
| 0,114 | 0,127 | 11,4 | 12,7 |
| 0,114 | 0,128 | 11,4 | 12,8 |
| 0,114 | 0,128 | 11,4 | 12,8 |
| 0,114 | 0,128 | 11,4 | 12,8 |
| 0,114 | 0,128 | 11,4 | 12,8 |
| 0,116 | 0,129 | 11,6 | 12,9 |
| 0,116 | 0,129 | 11,6 | 12,9 |
| 0,116 | 0,129 | 11,6 | 12,9 |
| 0,117 | 0,129 | 11,7 | 12,9 |
| 0,117 | 0,13 | 11,7 | 13 |
| 0,118 | 0,13 | 11,8 | 13 |
| 0,118 | 0,13 | 11,8 | 13 |
| 0,118 | 0,132 | 11,8 | 13,2 |
| 0,118 | 0,133 | 11,8 | 13,3 |
| 0,119 | 0,133 | 11,9 | 13,3 |
| 0,119 | 0,133 | 11,9 | 13,3 |
| 0,119 | 0,133 | 11,9 | 13,3 |
| 0,12 | 0,134 | 12 | 13,4 |
| 0,121 | 0,134 | 12,1 | 13,4 |
| 0,121 | 0,134 | 12,1 | 13,4 |
| 0,122 | 0,135 | 12,2 | 13,5 |
| 0,123 | 0,135 | 12,3 | 13,5 |
| 0,123 | 0,136 | 12,3 | 13,6 |
| 0,124 | 0,136 | 12,4 | 13,6 |
| 0,124 | 0,137 | 12,4 | 13,7 |
| 0,124 | 0,137 | 12,4 | 13,7 |
| 0,125 | 0,138 | 12,5 | 13,8 |
| 0,125 | 0,138 | 12,5 | 13,8 |
| 0,125 | 0,138 | 12,5 | 13,8 |
| 0,125 | 0,138 | 12,5 | 13,8 |
| 0,125 | 0,14 | 12,5 | 14 |
| 0,128 | 0,14 | 12,8 | 14 |
| 0,129 | 0,144 | 12,9 | 14,4 |
| 0,13 | 0,146 | 13 | 14,6 |
| 0,131 | 0,147 | 13,1 | 14,7 |
| 0,132 | 0,148 | 13,2 | 14,8 |
| 0,134 | 0,149 | 13,4 | 14,9 |
| 0,14 | 0,151 | 14 | 15,1 |
80 simulations de 10000 lancers :
| 10 000 lancers | |||
| fréquences | % | ||
| Obt9 | Obt10 | Obt9 | Obt10 |
| 0,1053 | 0,1178 | 10,53 | 11,78 |
| 0,1095 | 0,1183 | 10,95 | 11,83 |
| 0,1103 | 0,1185 | 11,03 | 11,85 |
| 0,1104 | 0,1189 | 11,04 | 11,89 |
| 0,1104 | 0,1195 | 11,04 | 11,95 |
| 0,1108 | 0,12 | 11,08 | 12 |
| 0,111 | 0,1203 | 11,1 | 12,03 |
| 0,1115 | 0,1205 | 11,15 | 12,05 |
| 0,112 | 0,1206 | 11,2 | 12,06 |
| 0,1122 | 0,121 | 11,22 | 12,1 |
| 0,1123 | 0,1211 | 11,23 | 12,11 |
| 0,1124 | 0,1213 | 11,24 | 12,13 |
| 0,1124 | 0,1214 | 11,24 | 12,14 |
| 0,1124 | 0,1217 | 11,24 | 12,17 |
| 0,1124 | 0,1218 | 11,24 | 12,18 |
| 0,1126 | 0,1219 | 11,26 | 12,19 |
| 0,1126 | 0,122 | 11,26 | 12,2 |
| 0,1128 | 0,1223 | 11,28 | 12,23 |
| 0,1129 | 0,1224 | 11,29 | 12,24 |
| 0,113 | 0,1229 | 11,3 | 12,29 |
| 0,1131 | 0,1229 | 11,31 | 12,29 |
| 0,1132 | 0,1229 | 11,32 | 12,29 |
| 0,1132 | 0,123 | 11,32 | 12,3 |
| 0,1133 | 0,1233 | 11,33 | 12,33 |
| 0,1137 | 0,1235 | 11,37 | 12,35 |
| 0,114 | 0,1235 | 11,4 | 12,35 |
| 0,1141 | 0,1236 | 11,41 | 12,36 |
| 0,1142 | 0,1238 | 11,42 | 12,38 |
| 0,1142 | 0,1238 | 11,42 | 12,38 |
| 0,1142 | 0,124 | 11,42 | 12,4 |
| 0,1145 | 0,124 | 11,45 | 12,4 |
| 0,1146 | 0,1242 | 11,46 | 12,42 |
| 0,1147 | 0,1244 | 11,47 | 12,44 |
| 0,1147 | 0,1244 | 11,47 | 12,44 |
| 0,1148 | 0,1245 | 11,48 | 12,45 |
| 0,1149 | 0,1245 | 11,49 | 12,45 |
| 0,115 | 0,1246 | 11,5 | 12,46 |
| 0,115 | 0,1247 | 11,5 | 12,47 |
| 0,115 | 0,1249 | 11,5 | 12,49 |
| 0,1154 | 0,125 | 11,54 | 12,5 |
| 0,1158 | 0,1251 | 11,58 | 12,51 |
| 0,1159 | 0,1251 | 11,59 | 12,51 |
| 0,1159 | 0,1252 | 11,59 | 12,52 |
| 0,116 | 0,1253 | 11,6 | 12,53 |
| 0,1164 | 0,1254 | 11,64 | 12,54 |
| 0,1165 | 0,1256 | 11,65 | 12,56 |
| 0,1166 | 0,1258 | 11,66 | 12,58 |
| 0,117 | 0,126 | 11,7 | 12,6 |
| 0,1171 | 0,1262 | 11,71 | 12,62 |
| 0,1172 | 0,1263 | 11,72 | 12,63 |
| 0,1172 | 0,1269 | 11,72 | 12,69 |
| 0,1172 | 0,127 | 11,72 | 12,7 |
| 0,1172 | 0,127 | 11,72 | 12,7 |
| 0,1173 | 0,1271 | 11,73 | 12,71 |
| 0,1173 | 0,1271 | 11,73 | 12,71 |
| 0,1175 | 0,1273 | 11,75 | 12,73 |
| 0,1175 | 0,1273 | 11,75 | 12,73 |
| 0,1177 | 0,1274 | 11,77 | 12,74 |
| 0,1178 | 0,1276 | 11,78 | 12,76 |
| 0,1178 | 0,1278 | 11,78 | 12,78 |
| 0,1179 | 0,128 | 11,79 | 12,8 |
| 0,118 | 0,1281 | 11,8 | 12,81 |
| 0,1182 | 0,1281 | 11,82 | 12,81 |
| 0,1182 | 0,1282 | 11,82 | 12,82 |
| 0,1183 | 0,1283 | 11,83 | 12,83 |
| 0,1183 | 0,1284 | 11,83 | 12,84 |
| 0,1185 | 0,1284 | 11,85 | 12,84 |
| 0,1188 | 0,1285 | 11,88 | 12,85 |
| 0,1189 | 0,1289 | 11,89 | 12,89 |
| 0,1191 | 0,1289 | 11,91 | 12,89 |
| 0,1191 | 0,1294 | 11,91 | 12,94 |
| 0,1196 | 0,13 | 11,96 | 13 |
| 0,1196 | 0,13 | 11,96 | 13 |
| 0,1198 | 0,1301 | 11,98 | 13,01 |
| 0,1198 | 0,1303 | 11,98 | 13,03 |
| 0,1201 | 0,1308 | 12,01 | 13,08 |
| 0,1207 | 0,1311 | 12,07 | 13,11 |
| 0,1218 | 0,1318 | 12,18 | 13,18 |
| 0,122 | 0,1328 | 12,2 | 13,28 |
| 0,1227 | 0,1331 | 12,27 | 13,31 |
Notes
| ↑1 | Cet énoncé est connu comme « problème de Galilée » ou comme « paradoxe du prince de Toscane». |
|---|---|
| ↑2 | Pour les personnes intéressées vous trouverez en annexe le code python qui a permis de réaliser ces simulations |
| ↑3, ↑4 | Données en pourcentage |
| ↑5 | Nous reprenons ces termes à Batanero C., Chernoff E.J., Engel J., Lee H.S., Sánchez E. (2016) Research on Teaching and Learning Probability. In: Research on Teaching and Learning Probability. ICME-13 Topical Surveys. Springer, Cham |
