Voici quelques démarches illustrées et animations qui permettent de retrouver les méthodes de calcul d’aire de certains polygones, méthodes souvent appelées formules d’aire.
Plus que les formules algébriques, nous aimerions que les élèves gardent en mémoire, pour chaque figure géométrique, les processus qui permettent de retrouver la méthode de calcul ou la formule (ce qui devrait revenir au même).
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
| Figures | Transformations (à retenir) | Formules |
Rectangle |  |  |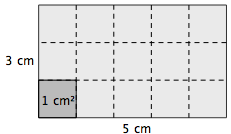
Parallélogramme  |  | |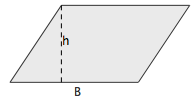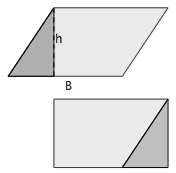
Transformations en mouvement
Les points en gras peuvent être bougés.
| Figure | Transformations (à retenir) | Formules |
Triangle  |   |   |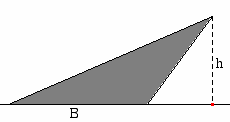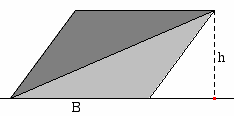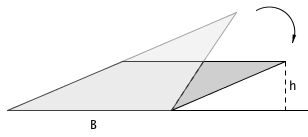
Transformations en mouvement
Les points en gras peuvent être bougés.
| Figure | Transformations (à retenir) | Formules |
Losange |  |  |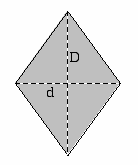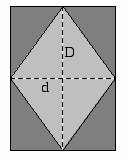
Transformations en mouvement
La formule de l’aire du losange est valable pour tous les quadrilatères dont les diagonales sont perpendiculaires.
Le point en gras peut être bougé.
| Figure | Transformations (à retenir) | Formules |
Trapèze |  |  |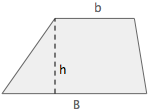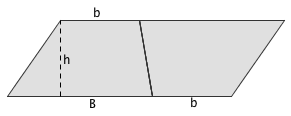
Transformations en mouvement
Instruments de pensée
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|