Voici une démonstration du théorème de Pythagore par les aires des parallélogrammes.
Public : 14 – 15 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
Théorème de Thalès dans un triangle.
Une droite coupant deux côtés d’un triangle est parallèle à la base si et seulement si elle découpe sur ces côtés des segments de longueurs proportionnelles.
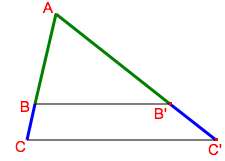
Autrement dit, étant donné un triangle ACC’, un point B appartenant à [AC] et un point B’ appartenant à [AC’], les droites BB’ et CC’ sont parallèles, si et seulement si
$$\small{\frac{\overline{BC}}{\overline{BA}}=\frac{\overline{B’C’}}{\overline{B’A}}}.$$
Démonstration par les aires de parallélogrammes
L’idée de cette démonstration, qui s’inspire de celle d’EUCLIDE (Les Eléments, proposition 2 du livre VI) est due, à notre connaissance, à Françoise VAN DIEREN.
Première partie
On suppose d’abord BB’ et CC’ parallèles. On veut en déduire que $\frac{\overline{BC}}{\overline{BA}}=\frac{\overline{B’C’}}{\overline{B’A}}.$
Plaçons un point quelconque F, différent de A, sur la droite parallèle à BB’ passant par A. Construisons les parallélogrammes AFDC et AFD’C’. La droite BB’ les coupe chacun en deux parallélogrammes.
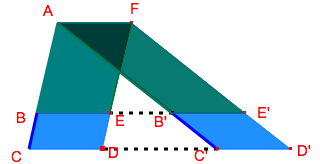
On a successivement
$$\small{\frac{\overline{BC}}{\overline{BA}}=\frac{\text{Aire} BCDE}{\text{Aire} ABEF}},$$
car le rapport des aires de deux parallélogrammes ayant même hauteur égale celui de leurs bases,
$$\small{\frac{\text{Aire} BCDE}{\text{Aire} ABEF}=\frac{\text{Aire} B’C’D’E’}{Aire A’B’E’F’}}$$
car deux parallélogrammes de même base ([BE], [AF] et [B’E’] ont même longueur) et de même hauteur ont même aire,
$$\small{\frac{\text{Aire} B’C’D’E’}{\text{Aire} A’B’E’F’}=\frac{\overline{B’C’}}{\overline{B’A}}},$$
car le rapport des aires de deux parallélogrammes ayant même hauteur égale celui de leurs bases.
Finalement ces trois égalités permettent de déduire que
$$\small{\frac{\overline{BC}}{\overline{BA}}=\frac{\overline{B’C’}}{\overline{B’A}}}.$$
Pour animer la figure suivante, bougez le point Mob.
Deuxième partie.
On suppose maintenant que $\frac{\overline{BC}}{\overline{BA}}=\frac{\overline{B’C’}}{\overline{B’A}}.$ On veut en déduire que BB’ et CC’ sont parallèles.
Plaçons un point quelconque F, différent de A, sur la droite parallèle à BB’ comprenant A. Construisons les parallélogrammes AFDC et AFD’C’. La droite BB’ les coupe chacun en deux parallélogrammes. Remarquons qu’on ne sait pas si D et D’ sont alignés avec C et C’ puisqu’on n’a pas encore montré que CC’ est parallèle à BB’.
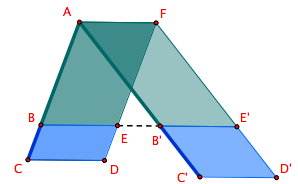
Par hypothèse, $$\small{\frac{\overline{BC}}{\overline{BA}}=\frac{\overline{B’C’}}{\overline{B’A}}}.$$
Par ailleurs
$$\small{\frac{\overline{BC}}{\overline{BA}}=\frac{\text{Aire}BCDE}{\text{Aire}ABEF}} \ \text{ et } \ \small{\frac{\text{Aire}B’C’D’E’}{AireA’B’E’F’}=\frac{\overline{B’C’}}{\overline{B’A}}},$$
car le rapport des aires de deux parallélogrammes ayant même hauteur égale celui de leurs bases,
On en déduit que
$$\small{\frac{\text{Aire}B CDE}{\text{Aire} ABEF}=\frac{\overline{BC}}{\overline{BA}} = \frac{\overline{B’C’}}{\overline{B’A}}=\frac{\text{Aire}B’C’D’E’}{\text{Aire}A’B’E’F’}},$$
et donc
$$\small{\frac{AireB CDE}{\text{Aire} ABEF}=\frac{\text{Aire}B’C’D’E’}{\text{Aire}A’B’E’F’}}.$$
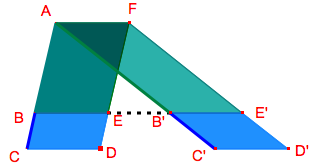
De plus, comme les parallélogrammes ABEF et AB’E’F ont la même base ([BE], [AF] et [B’E’] sont même longueur) et la même hauteur, ils ont la même aire. Donc les parallélogrammes BCDE et B’C’D’E’ ont aussi la même aire. Comme ils ont de plus des bases [BE] et [B’E’] de même longueur, ils ont forcément même hauteur.
Autrement dit, CC’ est parallèle à BB’.
Activités en amont
- Activité sur des familles de parallélogrammes à 12 – 14 ans
- Activité sur de comparaison et déformation de figures à 12 – 14 ans
- Une activité pour découvrir la démonstration du théorème de Thalès par les aires des parallélogrammes.
Instruments de pensée
- Mouvement, déformation de figures et familles de figures
- Changement de point de vue
- Isoler par la pensée
- Évoquer une situation intermédiaire
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|