On présente des pavages de parallélogrammes et des propriétés des angles qui apparaissent.
Public : 10-12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
1. Des pavages de parallélogrammes
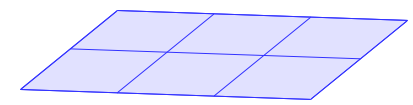
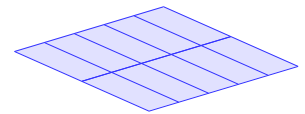
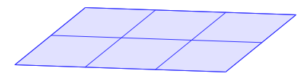
Voici des pavages de parallélogrammes superposables.
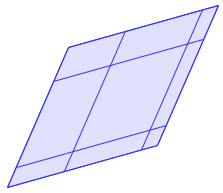
Et en voici un où les parallélogrammes ne sont pas superposables.
Dans un pavage de parallélogrammes,
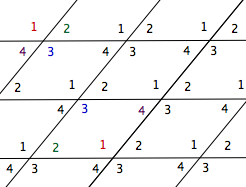
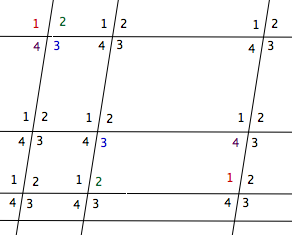
chaque nœud se répète par glissement, chaque nœud est le sommet d’un même agencement d’angles. On en déduit les propriétés suivantes :
- dans tous les parallélogrammes, les angles intérieurs opposés ont la même amplitude;
- dans chaque parallélogramme, la somme des amplitudes des angles est égale à 360°;
- dans chaque parallélogramme, la somme des amplitudes de deux angles consécutifs est égale à 180°.
2. Les angles autour du nœud
Les propriétés des angles situés autour d’un nœud :
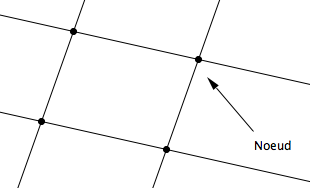
- la somme des amplitudes des angles autour d’un nœud est égale à 360°;
- les angles opposés par leur sommet ont la même amplitude;
- les angles sont disposés de façon régulière: un angle aigu est suivi d’un angle obtus, lui-même suivi d’un aigu, suivi d’un obtus;
- deux angles qui se suivent forment un angle plat.
3. Le mouvement dans des treillis
Lorsque l’on modifie l’inclinaison de certaines parallèles, les amplitudes des angles aigus varient tous de la même façon. Il en va de même pour les angles obtus.
Ce qu’un angle perd en amplitude est gagné par l’angle suivant.
Mais attention, si les droites ne sont pas parallèles, les amplitudes des angles ne varient pas toutes de la même façon.
Activités liées à ce contenu
Instruments de pensée
- Mouvement, déformation de figures.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|