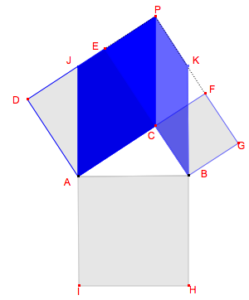
Il s’agit de retrouver les arguments d’une démonstration du théorème de Pythagore à partir d’une série de figures. Cette démonstration, inventée par Hermann Baravalle en 1945, fait intervenir une famille de parallélogrammes.
Public : 14 – 15 ans.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Déformer un parallélogramme ou un rectangle
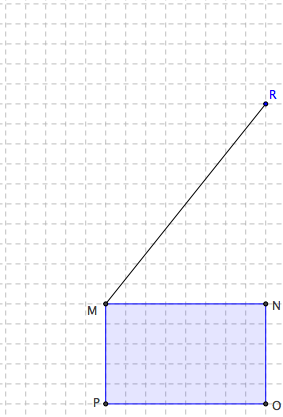
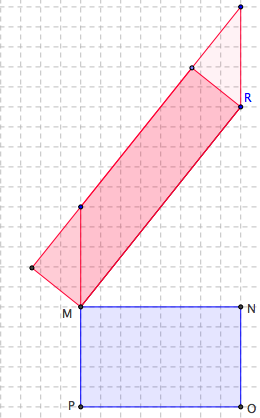
a) Sans rien mesurer, construisez sur [MR] un parallélogramme de même aire que le rectangle MNOP.
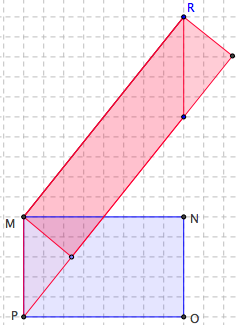
b) Sans rien mesurer, construisez sur [MR] un rectangle de même aire que le rectangle MNOP.
Solutions
a) On peut évoquer une famille de parallélogrammes de même aire ou la formule d’aire du parallélogramme et déformer le rectangle en prenant le côté [PM] comme base en conservant la hauteur correspondante.
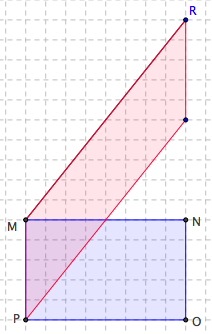
On peut aussi construire le parallélogramme « au-dessus » de [MR].
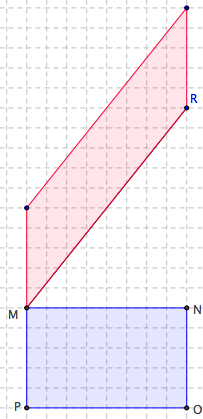
b) Ensuite, pour construire le rectangle demandé, il faut changer de point de vue et prendre [MR] comme base en conservant la hauteur correspondante. On peut à nouveau évoquer une famille de parallélogrammes de même aire, la formule d’aire du parallélogramme ou encore le fait de composer et décomposer.
D’un rectangle à l’autre
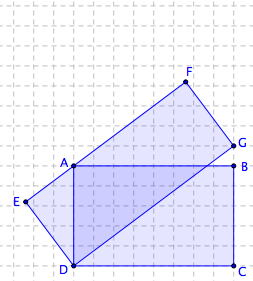
Les rectangles ABCD et EFGD ont la même aire. Vérifiez-le sans rien mesurer mais en construisant un parallélogramme qui a clairement la même aire que ces deux rectangles.
Solutions
On construit un parallélogramme de même aire que ces deux rectangles. On montre l’égalité d’aire en évoquant les mêmes arguments que précédemment.
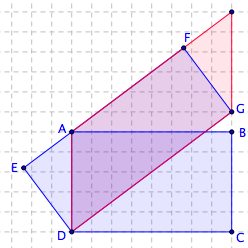
Théorème de Pythagore
Voici l’énoncé du théorème de Pythagore.
La somme des aires des carrés construits sur les côtés de l’angle droit d’un triangle rectangle est égale à l’aire du carré construit sur son hypoténuse.
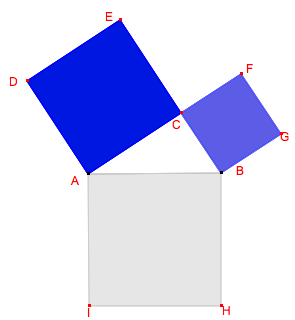
Démonstration du théorème de Pythagore
Il faut démontrer que, sur la figure ci-dessus, la somme des aires des carrés bleus égale l’aire du carré gris.
Voici les représentations de quatre étapes d’une démonstration du théorème de Pythagore, attribuée à Hermann Baravalle (1945). Retrouvez-en les arguments.

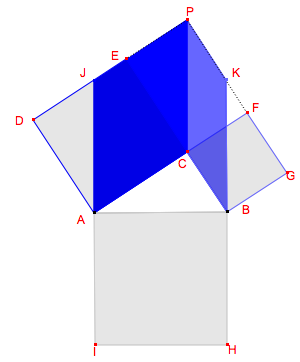
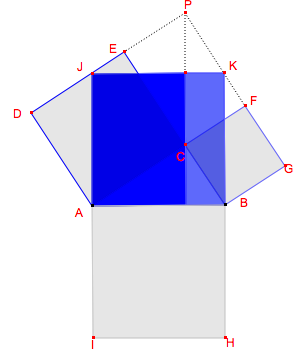
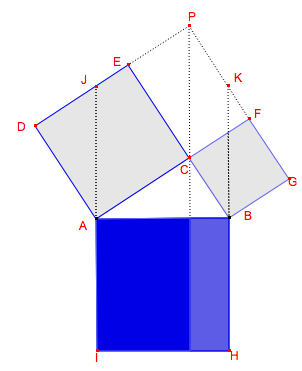
Solutions
Voir la démonstration du théorème de Pythagore par les aires des parallélogrammes
Activités en amont
- Activité sur des familles de parallélogrammes à 12 – 14 ans
- Activité sur de comparaison et déformation de figures à 12 – 14 ans
Contenu visé
- Une démonstration du théorème de Pythagore par les aires des parallélogrammes
Instruments de pensée
- Mouvement, déformation de figures et familles de figures
- Changement de point de vue
- Isoler par la pensée
- Évoquer une situation intermédiaire
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|