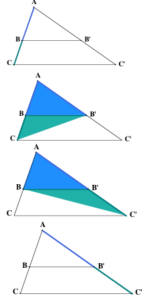
On utilise la comparaison d’aires de triangles pour démontrer le théorème de Thalès et sa réciproque, à la manière d’Euclide.
Public : 14 – 15 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Voici l’énoncé du théorème de Thalès (et de sa réciproque) dans un triangle.
Une droite coupant deux côtés d’un triangle est parallèle à la base si et seulement si elle découpe sur ces côtés des segments de longueurs proportionnelles.
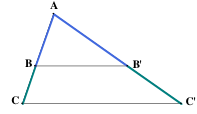
Cet énoncé recouvre deux propositions réciproques que l’on peut énoncer comme suit.
Proposition 1. Si une droite coupant deux côtés d’un triangle est parallèle à la base alors elle découpe sur ces côtés des segments de longueurs proportionnelles.
Proposition 2. Si une droite découpe sur deux côtés d’un triangle des segments de longueurs proportionnelles, alors elle est parallèle au troisième côté.
Pistes pour une démonstration
Proposition 1. On suppose d’abord BB’ et CC’ parallèles. On veut en déduire que
![]()
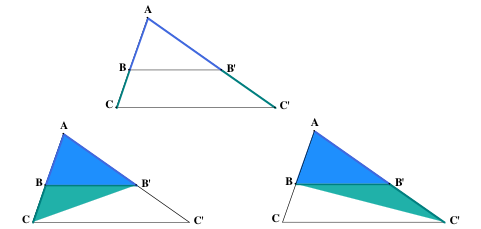
Les quatre figures suivantes sont la base de la démonstration d’EUCLIDE. Ne manquent que les arguments… Ecrivez-les.
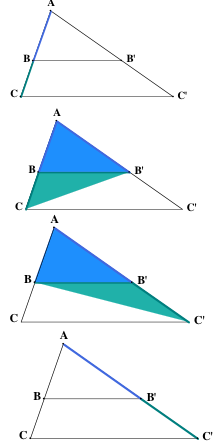
Proposition 2. On veut maintenant démontrer l’implication inverse. Voyez ce que l’on suppose, ce que l’on a déjà établi dans la première partie et qui peut nous être utile et ce que l’on veut en déduire.
Solution
Voir la démonstration du théorème de Thalès
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Activités en amont
Activités en aval
- Le théorème de Thalès par l’aire des triangles.
Instruments de pensée
- Mouvement et déformation de figures
- Changement de point de vue
- Se servir d’une situation intermédiaire