Les activités suivantes proposent de comparer des triangles de trois familles notamment selon leur aire et leur périmètre. Elles permettent notamment d’établir des propriétés sur l’aire des triangles.
Public : 12 – 14 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Des familles de triangles : découvertes
Matériel
Chaque groupe dispose de trois types de matériel (voir photos ci-dessous). Ce matériel est schématisé par les figures qui suivent.

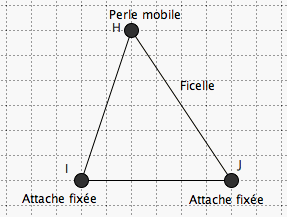
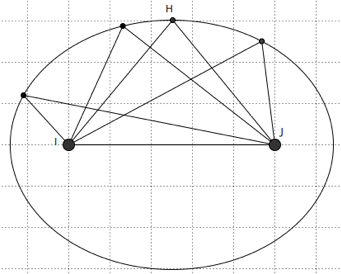
Le premier matériel est constitué d’une ficelle tendue passant par deux attaches parisiennes fixes (I et J) et sur laquelle est enfilée une perle mobile (initialement en H).
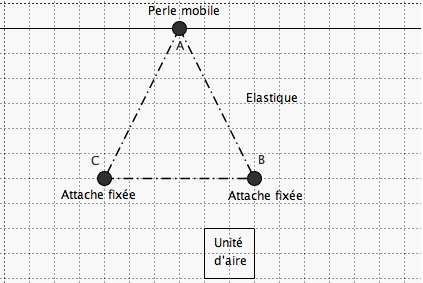
Le deuxième est constitué d’un élastique tendu passant par deux attaches parisiennes fixées (B et C) et par une perle (initialement en A) qui peut coulisser sur une pique à brochette fixée. Cette dernière est parallèle à BC.
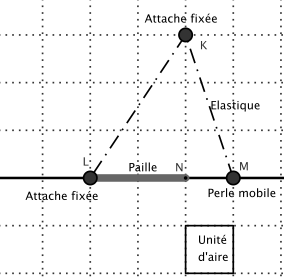
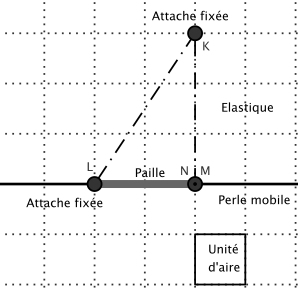
Le troisième comprend un élastique tendu passant par deux attaches parisiennes fixées (L et K) et par une perle (ici M) coulissant sur une pique à brochette fixée en L et N.
On a ajouté une paille sur la pique à brochette (segment [LN]) , pour que la perle ne se rapproche pas trop de l’attache parisienne L et pour qu’au départ l’élastique représente un triangle rectangle.
Dans chaque cas, on a glissé du papier quadrillé sur lequel on peut dessiner.
Comparez librement les triangles que l’on peut obtenir dans chaque cas.
Solution
Cette activité de constatation libre permet à l’enseignant de voir ou de revoir beaucoup
de notions telles que les caractéristiques des triangles liées aux angles ou aux côtés,
l’aire des triangles, leur périmètre, leur hauteur.
Des familles de triangles : aire et périmètre
- Reprenez la première maquette.
a) Comment obtenir le triangle de périmètre le plus petit ? Le plus grand ?
b) Comment obtenir le triangle d’aire la plus grande ? La plus petite ? - Reprenez la deuxième maquette.
Comment varient l’aire et le périmètre du triangle lorsqu’on déplace la perle ? - Reprenez la troisième maquette.
La perle est placée en N.
Où la placer pour doubler l’aire du triangle ?
Ou pour la tripler ?
Solutions
1. a) La première maquette présente une famille de triangles de même périmètre.
C’est la notion même de périmètre que l’on travaille donc ici.
b) Le fait que l’aire varie peut être comprise par l’examen de deux cas extrêmes,
lorsque la perle (H) est presque alignée avec les deux attaches (I et J) vers la gauche ou la droite.
L’aire est maximale lorsque la hauteur est la plus grande, la base étant fixée. Et on peut expérimenter que la hauteur est maximale lorsque le triangle est isocèle. La perle décrit la courbe représentée ci-dessous, appelée ellipse. On peut l’obtenir pratiquement en remplaçant la perle par une pointe de crayon.
2. Comme la pique à brochette est parallèle à la base du triangle, tous les triangles représentés ont la même aire.
On travaille à travers cette activité la proposition suivante :
si deux triangles ont la même base et les sommets opposés à cette base sur une droite parallèle à celle-ci, alors ils ont la même aire.
Le mouvement physique de la perle, prolongé par un mouvement mental, permet de parcourir cette famille de triangles.
On peut imaginer des triangles très « étirés » mais ayant tous la même aire que
le triangle initial ABC, ce qui ne va pas de soi.
Question de relance Et si on incline un peu la pique, comment
varie l’aire des triangles que l’on obtient ?
Par ailleurs, pour le périmètre, plus on éloigne la perle du point A plus le périmètre augmente. Il n’est pas évident de s’en convaincre lorsque la perle est très proche de A ; on pourrait croire que le périmètre reste constant. Par contre, on peut s’en persuader en éloignant de plus en plus la perle de A : on sent bien que l’élastique est de plus en plus tendu.
Pour que le périmètre reste constant, il faudrait que la perle décrive la courbe tracée ci-dessus à l’aide de la ficelle comme proposé avec le matériel 1.
3. La troisième maquette montre une famille de triangles dont l’aire et le périmètre augmentent à mesure que la perle M est tirée vers la droite.
Pour obtenir une aire double, il faut doubler (ou tripler) la base, puisque la hauteur est constante. On peut établir cela en utilisant la formule d’aire d’un triangle.
Ces questions mènent à la proposition suivante :
– si deux triangles ont la même hauteur, le rapport de leurs aires égale celui de leurs bases.
Activités en amont
- Représentations et déformations de triangles à 10-12 ans
- Familles de triangles à 10-12 ans
- Aire de triangles à 10-12 ans
Activités en aval
- Aire de triangles à 12-14 ans
- Partages d’aires à 12-14 ans
Instruments de pensée
Contenu visé
- Familles de triangles
- Aire de triangles (voir aussi Formules d’aire de quelques figures planes)
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|

