Nous proposons une activité pour introduire la propriété de la somme des amplitudes des angles intérieurs d’un triangle.
Public : 13-14 ans
| Retour au tableau d’accueil |
|---|
Activité
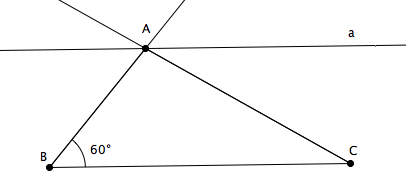
1. Sur la figure suivante, où la droite a est parallèle au côté [BC] du triangle ABC, on a indiqué l’amplitude d’un seul angle. Sans rien mesurer, pourriez-vous déterminer l’amplitude d’autres angles ? Justifiez.
2. Est-il possible de déterminer les amplitudes de tous les angles du dessin sachant que l’amplitude de l’angle C égale 50°? Justifiez.
3. Nommez tous les angles apparaissant sur le dessin.
Exprimez ensuite β en fonction de α et de γ . Justifiez.
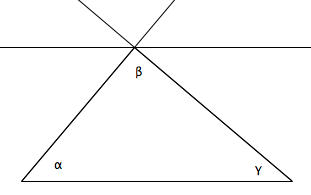
4. Énoncez la propriété de la somme des amplitudes des angles intérieurs d’un triangle.
Solutions
1. Les angles $B_1$ et $A_1$ sont correspondants donc $B_1$ = $A_1$.
Les angles $B_1$ et $A_2$ sont des angles alternes internes compris entre deux droites parallèles coupées par une sécante donc $B_1$ = $A_2$.
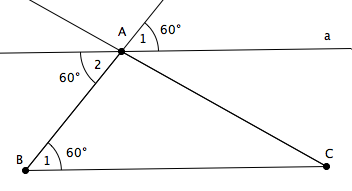
2. Oui, il est possible de déterminer l’amplitude de tous les angles du dessin.
Voici une justification possible :
Les angles $C_1$ et $A_4$ sont correspondants donc $A_4$ = $C_1$ = 50°.
De là, l’angle $A_3$ a une amplitude de 70° car les angles $A_1$ , $A_3$ et $A_4$ forment un angle plat
(180° – 60° – 50° = 70°).
Les angles $A_3$ et $A_5$ sont opposés par le sommet, donc $A_3$ = $A_5$.
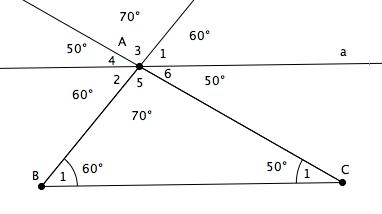
3. β = 180° – α – γ car α + β + γ = 60° + 70° + 50°=180°.
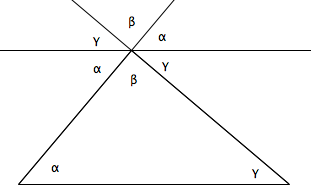
4. La somme des amplitudes des angles intérieurs d’un triangle égale 180°.
Activités en amont
Des angles dans tous leurs états
Activités en aval
Problèmes d’application sur les angles
Contenus visés
Somme des amplitudes des angles dans un triangle
Instruments de pensée
| Retour au tableau d’accueil |
|---|