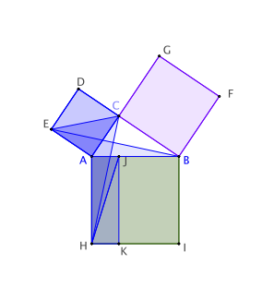
Voici une démonstration du théorème de Pythagore, très inspirée de celle d’Euclide (Les Eléments, Livre 1, Proposition 47).
Public : 14 – 15 ans.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Le Théorème de Pythagore
Pour tout triangle rectangle, la somme des aires des carrés construits sur les côtés de l’angle droit est égale à l’aire du carré construit sur l’hypoténuse.
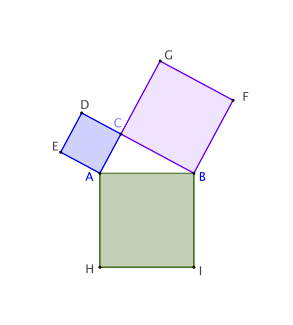
Démonstration
Considérons un triangle ABC rectangle en C et les carrés construits sur ses côtés.
Construisons J et K sur la parallèle à AH passant par C et tels que AJKH soit un rectangle.
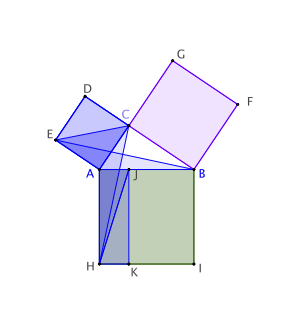
Nous allons montrer que le carré AEDC a même aire que le rectangle AJKH et que le carré CBFG a même aire que le rectangle BJKI.
Les triangles AEC et AEB ont même base ![]() et même hauteur
et même hauteur ![]() , car les droites BC et EA sont parallèles puisqu’elles sont toutes deux perpendiculaires à AC. Les triangles AEC et AEB ont donc même aire.
, car les droites BC et EA sont parallèles puisqu’elles sont toutes deux perpendiculaires à AC. Les triangles AEC et AEB ont donc même aire.
Le triangle ACH est l’image du triangle AEB par la rotation de 90° de centre A. En effet, en appliquant cette rotation, l’image de [AE] est [AC] et l’image de [AB] est [AH]. Ces deux triangles ont donc même aire.
Les triangles ACH et AJH ont même base ![]() et même hauteur
et même hauteur ![]() puisque KC (ou KJ) est parallèle à AH. Ces deux triangles ont donc même aire.
puisque KC (ou KJ) est parallèle à AH. Ces deux triangles ont donc même aire.
Finalement les triangles AEC et AJH ont la même aire, qui est la moitié de, respectivement, celle du carré AEDC et celle du rectangle AJKH.
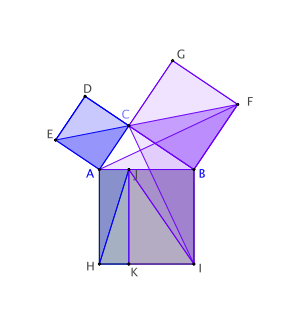
On peut montrer de la même façon que le carré CBFG a même aire que le rectangle BJKI :
- les triangles BFC et BFA ont même base
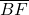 et même hauteur
et même hauteur 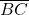 ,
, - le triangle BCI est image de BFA par une rotation de centre B,
- et enfin les triangles BCI et BJI ont même base
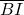 et même hauteur
et même hauteur 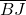 .
.
La somme des aires des carrés AECD et CBFG est égale à celle des aires des rectangles AJKH et BJKI, soit à l’aire du carré ABIH.
Activités en amont
- Vers la démonstration du théorème de Pythagore par les aires des triangles
Instruments de pensée
- Mouvement, déformation de figures et familles de figures
- Changement de point de vue
- Isoler par la pensée
- Évoquer d’une situation intermédiaire
Contenu visé
- La démonstration du théorème de Pythagore par les aires des triangles.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|