Vers une démonstration du théorème de Pythagore par les aires des triangles

Il s’agit de retrouver les arguments d’une démonstration du théorème de Pythagore présente dans Les Eléments d’Euclide (Livre 1, Proposition 47). Cette démonstration fait intervenir une famille de triangles et des instruments de pensée, tels le mouvement et le changement de point de vue.

Public : 14 – 15 ans.

Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans

Le Théorème de Pythagore

Pour tout triangle rectangle, la somme des aires des carrés construits sur les côtés de l’angle droit est égale à l’aire du carré construit sur l’hypoténuse.

Essayons de démontrer ce théorème.

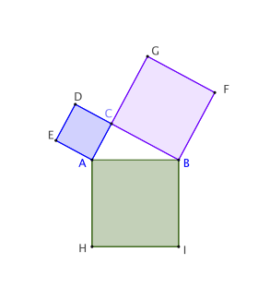
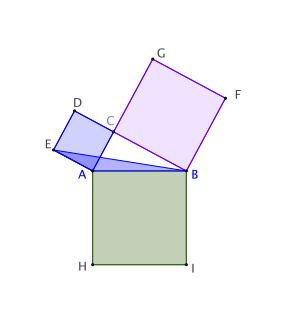
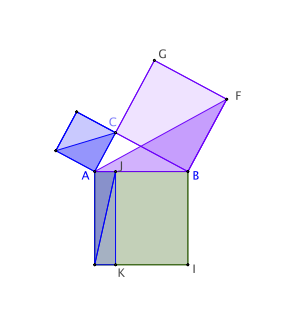
Soient un triangle ABC rectangle en C et les carrés construits sur ses côtés.
Euclide démontre que le carré AEDC a même aire qu’un certain rectangle que nous nommons AJKH.

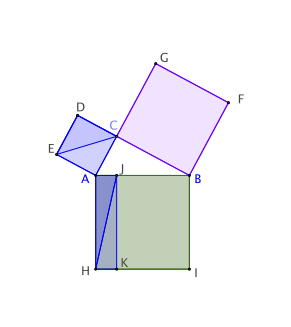
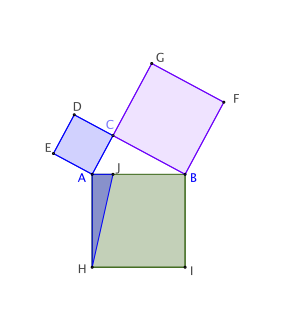
a) Voici en quelques images l’idée de sa démonstration. Retrouvez-en
les arguments. Précisez comment il faut construire le point J.

$Pythagore-Euclide0.png$
$Pythagore-Euclide1.png$
$Pythagore-Euclide3.png$
$Pythagore-Euclide2.png$
$Pythagore-Euclide5.png$
$Pythagore-Euclide4.png$

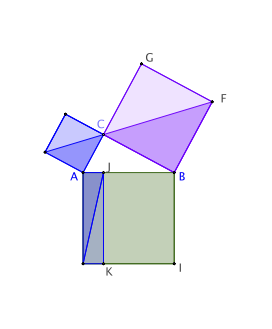
b) Démontrez de la même façon que le carré CBFG a même aire que le rectangle BJKI.

c) Pourquoi ne peut-on pas appliquer la même démarche si le triangle ABC n’est pas rectangle en C ?

Solutions

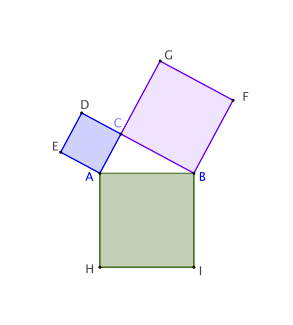
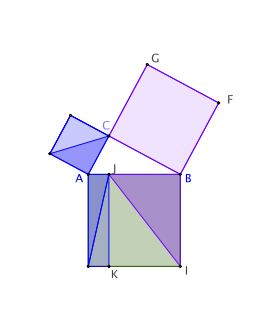
a) Les triangles AEC et AEB ont même base [AE] et même hauteur [AC]. Ils ont donc même aire.

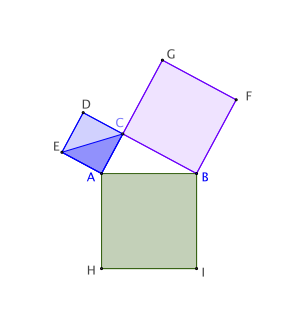
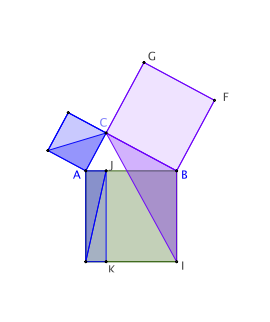
Le triangle ACH est l’image du triangle AEB par la rotation de 90° de centre A. Ces deux triangles ont donc même aire.

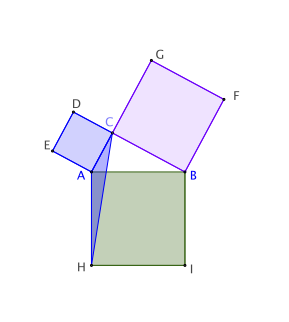
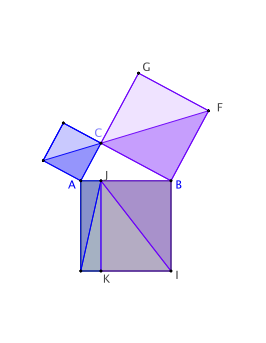
Les triangles ACH et AIH ont même base [AH] et même hauteur [AJ] donc même aire. Pour affirmer cela, il faut que CJ soit parallèle à AH

Finalement les triangles AEC et AJH ont donc la même aire, qui est la moitié de, respectivement, celle du carré AEDC et celle du rectangle AJKH.

b) On peut appliquer les même arguments aux triangles BFC et BFA de même base [BF] et de hauteur [BC], puis aux triangles BFA et BCI, dont l’un est image de l’autre par une rotation, et enfin aux triangles BCI et BJI de même base [BI] et de hauteur [BJ].