Lancer de deux dés

L’activité en bref

L’objectif est de trouver, à priori (à partir du calcul des possibilités) et à postériori (à partir des fréquences observées), les probabilités des différentes sommes obtenues en lançant deux dés.

Public cible

Toutes classes ayant dans leur programme l’étude des probabilités :

• 6GT, 6TT, 6TQ et 7^ème
• 2^ème secondaire pour l’étude des fréquences (matière du CE1D )

N’importe quelle autre classe intéressée par une approche des phénomènes aléatoires.

Enjeux

• Adopter une démarche expérimentale.
• Comprendre le lien entre fréquences et probabilités.
• Déterminer des probabilités à partir du calcul des possibilités.

Matériel

Deux dés par élèves.

Durée

Environ 3 heures de cours (4h si les élèves réalisent la simulation eux-mêmes).

Enoncé

Dans « Le devin », une aventure d’Astérix le Gaulois, un Gaulois se fait capturer par les Romains et tente de les convaincre qu’il n’est pas devin (voir l’extrait ci-dessous).

Croyez-vous qu’il s’agissait du bon choix pour le Gaulois ? Avait-il plus de chances d’obtenir VII plutôt qu’une autre somme ?

Répondons à ces questions étape par étape …

Étape 1 :

Chacun lance 20 fois deux dés en observant la somme des points. Notez vos résultats dans le tableau.

Résultat	1	2	3	4	5	6	7	8	9	10	11	12
Nombre de fois

A partir de vos résultats, croyez-vous que le choix du devin a été le bon ? Sinon qu’aurait-il dû choisir ?

Étape 2 :

Recueillons ensuite les résultats de tous les élèves de la classe (en prenant uniquement les résultats possibles). Y a-t-il un résultat qui apparait plus souvent que les autres ? Y a-t-il un résultat qui apparait moins souvent que les autres ? « 7 » était-il un bon choix pour le faux devin ?

Résultat	2	3	4	5	6	7	8	9	10	11	12
Élève 1
Élève  2
Élève 3
…
Élève 25

Étape 3 :

Si on globalise les observations de tous les élèves de la classe, quels sont les résultats qui apparaissent le plus souvent ? Le moins souvent ? Avez-vous une explication à donner ?

Résultat	2	3	4	5	6	7	8	9	10	11	12
Classe

Étape 4 :

Réalisez le graphique des effectifs des sommes obtenues par votre classe (sur papier quadrillé ou Excel).

Étape 4bis (facultative) :

Voici ci-dessous les résultats de toutes les classes de l’école ayant participé à l’expérience.

Résultat	2	3	4	5	6	7	8	9	10	11	12
Classe

Comment pourrions-nous comparer les résultats de votre classe à ceux de toutes les classes ?

Faites un graphique en bâtonnets comparatif reprenant votre classe et l’ensemble de toutes les classes (sur Excel ou sur une feuille à part).

Que pouvez-vous dire de l’allure du graphe en bâtonnets  ?

Étape 5 version 1: pour des  élèves ayant des cours de programmation ou habitués à scratch ou python)^[1]En annexe : exemple de code scratch et python:

Que se passe-t-il quand on lance un très grand nombre de fois les deux dés?

Plutôt que de les lancer, nous allons faire une simulation à l’aide d’un logiciel.

Il s’agit donc d’écrire un programme « scratch » ou « python » permettant de lancer un grand nombre de paires de dés.

Déterminez les fréquences des différentes sommes (aux millièmes près).

Voyez-vous des similitudes dans les fréquences d’apparitions des sommes?

La fréquence de la “somme 7” vous fait-elle penser à quelque chose?

Étape 5 version 2: avec la simulation réalisée :

Que se passe-t-il quand on lance un très grand nombre de fois les deux dés?

Plutôt que de les lancer, nous allons faire une simulation à l’aide d’un logiciel.

Approchons-nous de la probabilité des sommes des deux dés à l’aide d’une simulation.

Voici les effectifs obtenus pour une simulation de 1 million de lancers de deux dés.

Somme des deux dés	Effectif des différentes sommes sur 1 000 000
2	27584
3	55662
4	83329
5	111249
6	138504
7	166229
8	139698
9	110851
10	83120
11	55799
12	27975

Calculer les fréquences aux millièmes près :

Somme des deux dés	Fréquence des différentes sommes
2
3
4
5
6
7
8
9
10
11
12

Voyez-vous des similitudes dans les fréquences d’apparitions des sommes?

La fréquence de la “somme 7” vous fait-elle penser à quelque chose?

Pouvez-vous en déduire les chances de chacune des sommes et donner une conclusion sur le choix du devin?

Voir ci-dessous le fichier pdf de l’activité:

Éléments de réponse et quelques commentaires didactiques

Étape 1 :

Les élèves devraient se rendre compte qu’il est impossible d’obtenir 1 en sommant deux faces de dés. On peut ainsi définir la notion d’événement impossible si la notion n’a pas été vue. On peut également aborder les notions d’événements possibles et certains si l’activité est utilisée comme introduction du chapitre sur les probabilités. Généralement, certains élèves auront obtenu beaucoup de fois la somme 7 et d’autres peu, voire aucune fois. Il est donc difficile à ce stade de dire si 7 est un mauvais choix ou non.

Pour accélérer la prise de notes des résultats, les élèves peuvent se mettre par deux avec l’un qui lance et l’autre qui prend note.

Étapes 2, 3 et 4 :

Les sommes les plus fréquentes seront généralement les sommes médianes (5,6,7,8,9). Il est intéressant à ce stade de demander aux élèves pourquoi selon eux ce sont ces sommes qui reviennent le plus et noter toutes leur hypothèses (même celles qui paraissent erronées et qui seront discutées dans la suite).

La notion d’effectif est normalement connue des élèves mais il est utile de s’assurer que ce soit bien le cas .

Pour la réalisation du graphique, il n’est pas précisé de faire un graphique en bâtonnets et ce, dans le but de créer le débat. En effet, il peut être intéressant de voir si certains élèves choisissent, par exemple, de faire un graphique à points reliés. Ce qui ouvre la discussion quant à la pertinence on non de relier les points.

Étape 4bis :

Cette étape n’est possible que si vous expérimentez cette activité dans plusieurs classes. Ce sera à vous de compléter le tableau en fonction des résultats obtenus dans toutes vos classes. 

La question: “Comment pourrions-nous comparer les résultats de votre classe à ceux de toutes les classes ?” a pour but que les élèves proposent d’eux mêmes de déterminer les fréquences des sommes obtenues pour comparer leur classe à l’ensemble des élèves.

L’intérêt de l’activité est de comparer les situations avec peu ou beaucoup de lancers de dés (un exemple est donné ci-dessous).

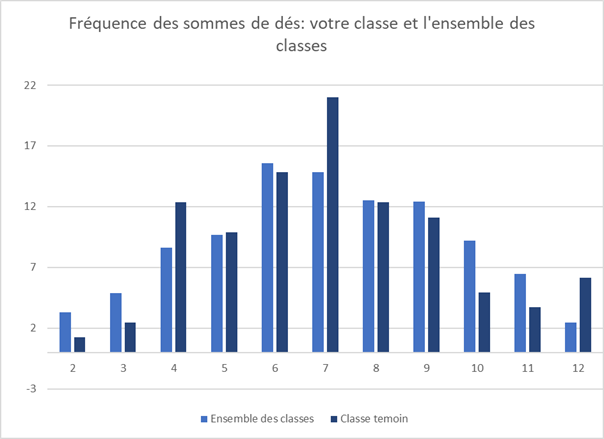
La question: “Que pouvez-vous dire de l’allure du graphe en bâtonnets?” permet de conclure que la courbe qui relie le sommet des bâtonnets du groupe ensemble des classes est plus lisse que celle de la classe témoin.

La notion de fréquence est normalement connue des élèves mais il est bien de leur rappeler ce mot de vocabulaire si ils formulent cette notion autrement car ce terme est utilisé dans les étapes suivantes.

Étape 5 :

Pour la question: “Que se passe-t-il quand on lance un très grand nombre de fois les deux dés?” , nous espérons que les élèves proposent d’eux mêmes la notion de probabilité. Soit parce qu’ils ont déjà travaillé sur l’aspect fréquentiste des probabilités soit en généralisant par rapport à la stabilisation des fréquences avec le nombre de lancers qui augmente.

Le tableau ci-dessous nous donne un exemple des fréquences que nous pouvons obtenir.

Somme des deux dés	Fréquence
2	0,028
3	0,056
4	0,083
5	0,111
6	0,139
7	0,166
8	0,140
9	0,111
10	0,083
11	0,056
12	0,028

• On constate que certaines fréquences sont très proches. Si on note « 2 », l’événement « avoir 2 », P(2) évalue les chances d’obtenir 2, à savoir la probabilité de cet événement. À partir du tableau résultant de la simulation, on peut conjecturer que: P(2) = P(12) ; P(3) = P(11) ; P(4) = P(10) ; P(5) = P(9) ; P(6) = P(8). On peut ainsi définir la notion d’évènements équiprobables.

• La fréquence de 7 (0,166) est très proche de la fréquence de chacune des faces en lançant un seul dé. On peut donc conjecturer que P(7) = 1/6

Nous supposons dans cet article que les élèves ont déjà été confrontés à la notion de probabilité et de son approche fréquentiste dans la cadre de l’étude du lancer de dé unique, ou d’un autre problème simple.

Comment pourrait-on justifier que P(7) = 1/6 ?

Voici une suggestion de procédure…

Quelles sont les sommes possibles pour avoir 7 ?

2+5, 3+4, 1+6

Quels sont les sommes possibles pour avoir 8 ?

2+6, 3+5, 4+4

Pourtant grâce à la simulation, nous savons que 7 apparaît plus fréquemment que 8.

C’est qu’il faut distinguer une somme comme 4+4 (qui ne peut s’obtenir que d’une façon avec deux dés   qui affichent 4) d’une somme comme 2+5 (qui peut s’obtenir de deux façons : un 2 avec le premier dé et un 5 avec le second ou le contraire).

Voici donc les possibilités détaillées pour la somme 7 et la somme 8 :

Avoir 7 ?

2+5, 3+4, 1+6, 5+2, 4+3 et 6+1 (6 possibilités).

Avoir 8 ?

2+6, 3+5, 4+4, 6+2 et 5+3 (5 possibilités).

Nous savons donc que  P(7) =  6/nombre total de possibilités = 1/6.

Il semblerait raisonnable de penser qu’il y a en tout 36 possibilités.

De la même manière, on peut déterminer les autres probabilités :

Avoir 2 : 1+1 (1 possibilité ) : P(2) = 1/36 = P(12)

Avoir 3 : 1+2,2+1 (2 possibilités ) : P(3) = 2/36 =1/18 = P(11)

Avoir 4 : 2+2,3+1,1+3 (3 possibilités ) : P(4) = 3/36 = 1/12 = P(10)

Avoir 5 : 2+3,3+2,1+4,4+1 (4 possibilités ) : P(5) = 4/36 = 1/9 = P(9)

Avoir 6 : 3+3,2+4,4+2,1+5,5+1 (5 possibilités ) : P(6) = 5/36 = P(8)

Avoir 7 : 1+6,6+1,2+5,5+2,3+4,4+3 (6 possibilités ) : P(7) = 6/36 = 1/6

Une autre façon de procéder est de réaliser le tableau des sommes obtenues afin de comptabiliser l’effectif de chaque somme.

+	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Quelques échos des classes

L’activité a été testée dans deux classes de 6TQ, une classe de 7PC et une classe de 2^ème différenciée

Pour avoir de plus amples informations sur les échos des classes, voir le rapport d’observation ci-dessous (certains énoncés apparaissent dans leur version première et ont été retravaillés depuis ces expérimentations).

Le sel du problème

Cette activité permet de faire le lien entre fréquences et probabilités (dans le programme de 6^ème secondaire) au travers d’une expérience dont les événements élémentaires ne sont pas équiprobables et dont les probabilités sont donc un peu moins évidentes à cerner. Il s’agit à la fois d’une approche fréquentiste des probabilités et d’une approche classique par les combinaisons.^[2]Nous reprenons les termes de fréquentiste et de classique à Batanero C., Chernoff E.J., Engel J., Lee H.S., Sánchez E. (2016) Research on Teaching and Learning Probability. In: Research on … Continue reading

Elle permet également aux élèves d’émettre des hypothèses et ainsi de créer le débat entre eux.

Annexe

Code python :

import random # importation du module de création de nombre aléatoire

print(“Ce code permet de simuler de(le) lancers de paire de dés”)

Nbr_Lancer = int(input(“Combien de lancers, voulez-vous effectuez”))

# les compteurs de sommes (de 2 à 12)

C2 = 0

C3 = 0

C4 = 0

C5 = 0

C6 = 0

C7= 0

C8 = 0

C9 = 0

C10 = 0

C11 = 0

C12 = 0

for i in range (Nbr_Lancer): # je fais toutes mes lancés(lancers)

    Des1 = random.randint(1, 6)

    Des2 = random.randint(1, 6)

    Somme = Des1 + Des2

    #le compteur en question augmente si sa face apparait

    if Somme ==2:

        C2 = C2+1

    elif Somme ==3:

        C3 = C3+1

    elif Somme  ==4:

        C4 = C4+1

    elif Somme  ==5:

        C5 = C5+1

    elif Somme  ==6:

        C6 = C6+1

    elif Somme  ==7:

        C7 = C7+1

    elif Somme  ==8:

        C8 = C8+1

    elif Somme  ==9:

        C9 = C9+1

    elif Somme  ==10:

        C10 = C10+1

    elif Somme  ==11:

        C11 = C11+1

    elif Somme  ==12:

        C12 = C12+1

print(“Nombre de fois que j’ai obtenu une somme égale à 2:”, C2)

print(“Nombre de fois que j’ai obtenu une somme égale à 3:”, C3)

print(“Nombre de fois que j’ai obtenu une somme égale à 4:”, C4)

print(“Nombre de fois que j’ai obtenu une somme égale à 5:”, C5)

print(“Nombre de fois que j’ai obtenu une somme égale à 6:”, C6)

print(“Nombre de fois que j’ai obtenu une somme égale à 7:”, C7)

print(“Nombre de fois que j’ai obtenu une somme égale à 8:”, C8)

print(“Nombre de fois que j’ai obtenu une somme égale à 9:”, C9)

print(“Nombre de fois que j’ai obtenu une somme égale à 10:”, C10)

print(“Nombre de fois que j’ai obtenu une somme égale à 11:”, C11)

print(“Nombre de fois que j’ai obtenu une somme égale à 12:”, C12)

print(“Fréquence d’avoir une somme de 2:”, C2/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 3:”, C3/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 4:”, C4/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 5:”, C5/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 6:”, C6/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 7:”, C7/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 8:”, C8/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 9:”, C9/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 10:”, C10/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 11:”, C11/Nbr_Lancer)

print(“Fréquence d’avoir une somme de 12:”, C12/Nbr_Lancer)

Code scratch :

https://scratch.mit.edu/projects/464028439/