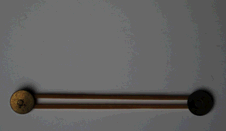Représentations et déformations de triangles

Public : 10 – 12 ans

Retour au tableau d’accueil
Une géométrie articulée de 10 à 15 ans

Constructions libres

Matériel : un élastique fermé, deux punaises, un support.

Tendez l’élastique entre deux punaises fixées comme sur la photo suivante pour représenter un segment. Les punaises représentent deux sommets d’un triangle. Tirez sur l’élastique pour représenter un triangle.

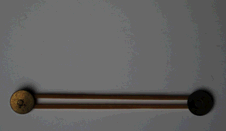
Modifiez la configuration pour que ce triangle soit successivement
– isocèle,
– équilatéral,
– rectangle,
– rectangle isocèle.

Solutions

L’objectif de cette activité n’est pas de trouver toutes les configurations pratiques et théoriques répondant aux conditions imposées. On ne demande pas non plus une précision telle qu’il serait nécessaire de mesurer les côtés et les angles.
Par contre, l’activité constitue une occasion d’exprimer la signification des adjectifs « isocèle », « équilatéral », « rectangle ».

Voici une configuration représentant à peu près un triangle isocèle.

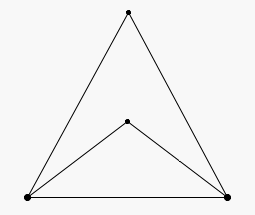
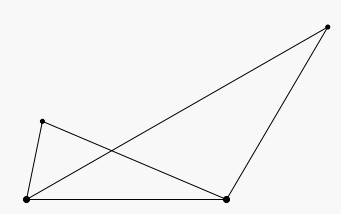
La recherche de solutions variées favorise le changement de point de vue. On perçoit rapidement que les deux triangles représentés sur la figure ci-dessous sont isocèles. C’est moins évident pour ceux de la figure suivante.

De même, on percevra rapidement que les deux triangles ci-dessous sont rectangles. C’est moins évident pour ceux de la figure suivante.

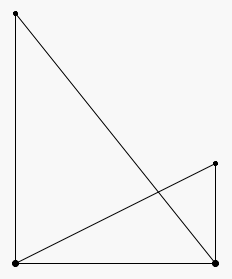
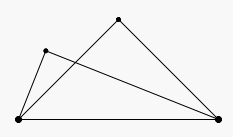
Doubler l’aire

Matériel : un élastique fermé, trois punaises, un triangle en carton, un support quadrillé.

Placez le triangle en carton sur le support. Fixez une punaise en chacun de ses sommets. Tendez l’élastique entre les trois punaises fixées comme sur la photo suivante pour que l’élastique se superpose aux côtés du triangle. Tirez sur l’élastique pour doubler l’aire de la figure qu’il délimite.

Solutions

Certaines solutions consistent à former un quadrilatère en utilisant un deuxième triangle identique au triangle donné. Il s’agit de parallélogrammes (trois solutions) et de cerfs-volants (trois solutions). Les deux photos suivantes illustrent deux de ces cas. Ces démarches ne nécessitent pas de recourir à des formules d’aire : ces quadrilatères sont composés de deux triangles superposables.

Si on a déjà abordé la formule d’aire du triangle, on peut aussi doubler un côté, une base, en conservant la même hauteur, comme illustré sur la figure ci-dessous. Mais les deux triangles qui apparaissent ne sont pas superposables.