Nous proposons ici des problèmes nécessitant l’utilisation des différents types d’angles et la propriété de la somme des amplitudes des angles intérieurs d’un triangle.
Public : 13-14 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
On propose les problèmes suivants après avoir établi la propriété de la somme des angles d’un triangle.
Activité 1
Les figures suivantes sont constituées de deux droites parallèles a et b et de sécantes. Déterminez, dans chacun des cas, l’amplitude de l’angle α. Justifiez.
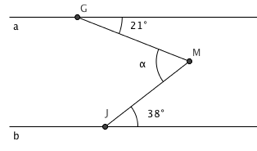
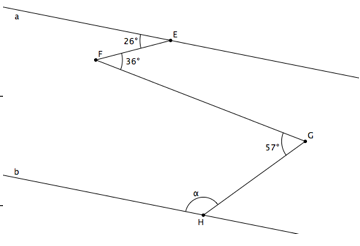
Solution
Une solution est de tracer une droite parallèle aux droites a et b comprenant le point M. Des angles alternes internes, de même amplitude sont alors déterminés. L’amplitude de l’angle α est égale à 59° (21° + 38°).
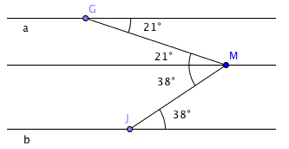
Une deuxième solution est de déterminer des triangles rectangles et de calculer la somme des amplitudes des angles en chaque triangle.
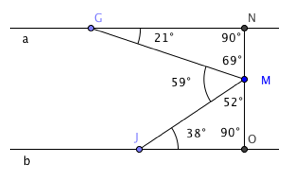
Une troisième solution est de déterminer des triangles isocèles et de calculer la somme des amplitudes des angles en chaque triangle.
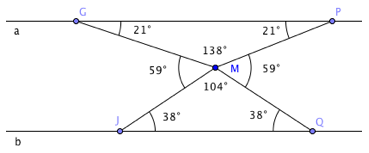
Une quatrième solution est de prolonger le segment [JM]. L’amplitude de l’angle α égale 59 ° (21° + 38°) en vertu de la propriété suivante : l’amplitude d’un angle extérieur à un triangle est égale à la somme des amplitudes des angles intérieurs non adjacents à l’angle.
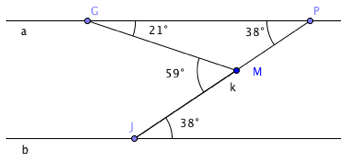
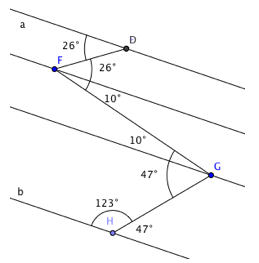
Pour la deuxième figure, une solution consiste à tracer deux droites parallèles aux droites a et b, l’une comprenant le point F et l’autre comprenant le point G.
Activité 2
Activité 2
En assemblant les côtés de deux triangles, construisez un trapèze. Ne prenez aucune mesure. Basez-vous sur les mesures indiquées.
Exemple :
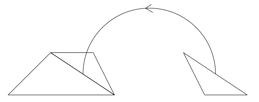
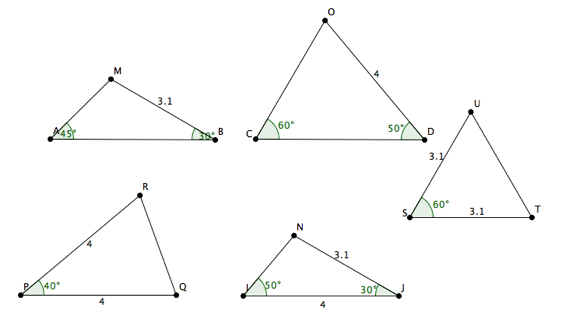
Solution
Il faut faire correspondre pour un premier trapèze le côté [IJ] avec le côté [OD]. La figure obtenue est un trapèze car les angles alternes internes ont même amplitude, donc les côtés [CD] et [ON] sont parallèles.
On obtient un deuxième trapèze en faisant correspondre le côté [NJ] avec le côté [BM]. La justification est similaire.
Activités en amont
- Déformation de quadrilatères
- Des angles dans tous leurs états
- Somme des amplitudes des angles intérieurs d’un triangle
Contenus visés
Instruments de pensée
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|

