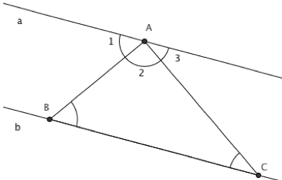
Sont repris ici l’énoncé et une démonstration de la propriété des angles dans un triangle.
Public : 13-14 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Propriété : Dans tout triangle, la somme des amplitudes des angles intérieurs égale 180°.
Démonstration.
Soit le triangle ABC. Traçons une droite a parallèle au côté [BC] du triangle et comprenant le point A. Cette droite détermine des angles A1, A2 et A3 qui forment ensemble un angle plat ; on peut donc écrire que
A1 + A2 + A3 = 180°.
Or, on voudrait prouver que
B + A2 + C = 180°.
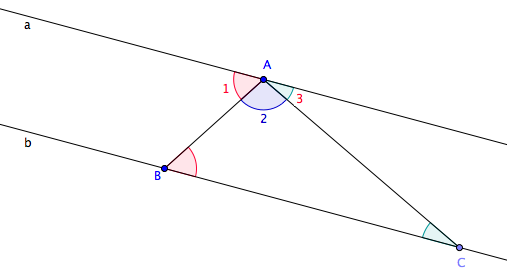
Les angles B et A1 sont de même amplitude car ce sont des angles alternes internes déterminés par les parallèles a et BC et la sécante AB. On obtient l’égalité suivante : B = A1.
Les angles C et A3 sont également alternes internes déterminés par les parallèles a et BC et la sécante AC et sont donc de même amplitude.
On a C = A3.
Dès lors, en remplaçant l’angle A1 par l’angle B et l’angle A3 par l’angle C dans l’égalité
A1 + A2 + A3 = 180°,
on obtient une nouvelle égalité :
B + A2 + C = 180°.
Ce qu’il fallait démontrer.
Activité liée à ce contenu
- Des angles dans tous leurs états (partie 6)
- Somme des amplitudes des angles intérieurs d’un triangle
- Problèmes d’application sur les angles
Contenus liés
Instruments de pensée
- Changement de point de vue
- L’astuce de cette démonstration (tracer une parallèle au côté [AB]) nécessite de voir l’invisible
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|