Les deux activités proposées permettent de mettre en jeu les familles de triangles de même aire et de même base.
Public : 10 – 12 ans.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
Activité 1 : Créer une famille de triangles d’aires égales
a) Trouve un point C pour que le triangle ABC ait une aire de 12,5 cm![]() .
.
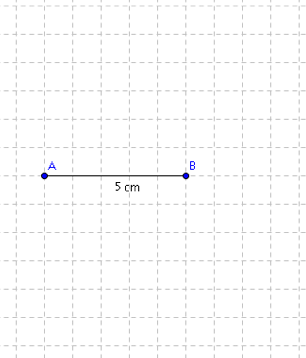
b) Sur la même figure, trouve d’autres possibilités. Trouves-en beaucoup.
c) Sur la même figure, trouve tous les endroits où on peut placer le point D pour que le triangle ABD ait une aire de 12,5 cm2.
Solutions
La hauteur doit mesurer 5 cm. Voici quelques solutions :
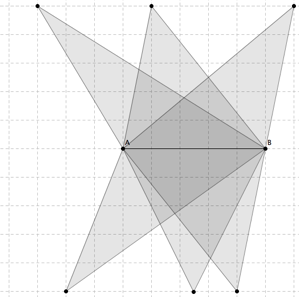
L’ensemble de tous les points C qui conviennent est constitué de deux droites parallèles à la base [AB]. Pour modifier la figure, bougez les points rouges.
Conclusion : deux triangles de même base et de même aire ont leur troisième sommet sur une droite parallèle à leur base commune.
Activité 2. Déformer en conservant l’aire
1. Imaginons que sur la figure suivante, le point C puisse bouger en déformant le triangle ABC (A et B restent fixes).
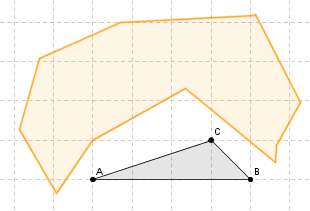
2. Colorie la partie de la zone jaune où on peut placer le point C
– pour que l’aire du triangle ABC augmente (en orange),
– pour que l’aire du triangle ABC ne varie pas (en bleu),
– pour que l’aire du triangle ABC diminue (en turquoise).
Solutions
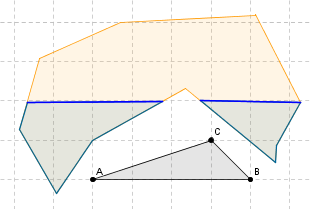
Vérification dynamique (lien ci-dessous) : amène le point C dans la zone orange sans changer l’aire du triangle ABC.
Activités en amont
Représentations et déformations de triangles
Familles de triangles à 10-12 ans
Trois formes de la formule d’aire des triangles
Activités en aval
Dissections géométriques à 10-12 ans
Familles de triangles à 12-14 ans
Instruments de pensée
Mouvement et déformation de figures
Contenu visé
Aire de triangles.
Ce contenu intervient dans la démonstration du théorème de Thalès par les aires de triangles et dans la démonstration du théorème de Pythagore par les aires des triangles.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |

