Voici une démonstration du théorème de Pythagore, due à Hermann Baravalle (1945). Elle constitue une occasion d’utiliser des familles de parallélogrammes et d’appliquer des instruments de pensée tels que le mouvement ou le changement de point de vue.
Public : 14 – 15 ans.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Théorème de Pythagore
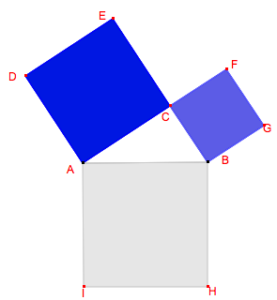
La somme des aires des carrés construits sur les côtés de l’angle droit d’un triangle rectangle est égale à l’aire du carré construit sur son hypoténuse.
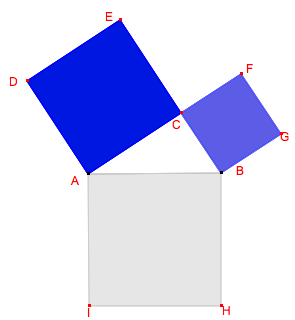
Démonstration
Nous allons montrer que, sur la figure ci-dessus, la somme des aires des carrés bleus égale l’aire du carré gris. Pour cela, nous allons déformer ces deux carrés bleus en parallélogrammes, puis en rectangles, tout en conservant leur aire, pour recouvrir exactement le grand carré gris.
Voici les trois grandes étapes de la démonstration.
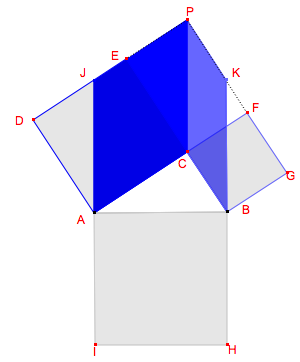
1. Les deux carrés bleus ci-dessus ont respectivement la même aire que les deux parallélogrammes bleus JPCA et PKBC ci-dessous. En effet, le carré DECA et le parallélogramme JPCA ont la même base [AC] et la même hauteur [DA]. De même le carré FGBC a même aire que le parallélogramme PKBC car ils ont même base [CB] et même hauteur [GB].
2. Les parallélogrammes bleus JPCA et PKBC ci-dessus ont respectivement la même aire que les rectangles bleus ci-dessous. En effet, le parallélogramme JPCA et le rectangle correspondant ont même base [JA] et même hauteur. De même le parallélogramme PKBC et le rectangle correspondant ont même base [BK] et même hauteur.
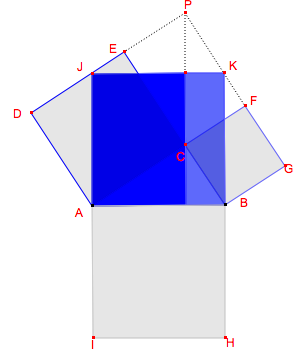
3. Les deux rectangles bleus forment ensemble un carré de côté [AJ] égal à [AB]. Ce carré se superpose donc bien au carré [AB].
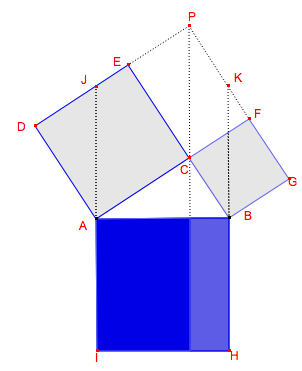
La somme des aires des deux carrés bleus égale donc l’aire du grand carré gris.
Notons que certains éléments de cette démonstration ont été laissés dans l’ombre. Il est d’ailleurs étonnant que les hypothèses du théorème n’aient pas été explicitement utilisées.
Introduisons ces parties restées dans l’ombre par deux questions :
a) Comment se fait-il qu’après les premières déformations des deux carrés bleus, nous obtenions deux parallélogrammes parfaitement accolés, ayant deux sommets communs P et C ?
b) Après la transformation des parallélogrammes en rectangles, ces derniers forment-ils bien un carré superposable à ABHI ?
Pour répondre à ces deux questions, montrons que les segments [JA] et [KB] ont la même longueur que [AB].
Pour cela, intéressons-nous au triangle JDA. Il est isométrique à ABC. En effet les angles en D et en C sont droits, les côtés [AD] et [AC] sont de même longueur et, vu que les angles JAB et DAC sont tous les deux droits, les angles DAJ et CAB des deux triangles sont de même amplitude (ils sont complémentaires du même angle JAC). Les côtés [JA] et [AB] sont donc de même longueur.
On peut raisonner de la même façon pour montrer que le triangle KBG est isométrique à ABC et donc que les côtés [KB] et [AB] sont de même longueur.
Les deux parallélogrammes ont donc bien un côté [PC] commun. Et celui-ci est bien de même longueur que [AB].
On a donc bien eu besoin des hypothèses : l’angle en C doit être droit et les deux quadrilatères sur [AC] et [CB] doivent être des carrés.
Activités en amont
- Activité sur des familles de parallélogrammes à 12 – 14 ans
- Activité sur Comparaison et déformation de figures à 12 – 14 ans
- Vers une démonstration du théorème de Pythagore par les aires de parallélogrammes.
Instruments de pensée
- Mouvement, déformation de figures et familles de figures
- Changement de point de vue
- Isoler par la pensée
- Évoquer une situation intermédiaire
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|