Au fil de sa scolarité, l’apprenant élargit progressivement l’univers des nombres qu’il connaît : il appréhende des nombres naturels de plus en plus grands d’abord, puis des fractions, des nombres décimaux, et d’autres encore, comme les entiers négatifs à l’école secondaire. A chaque fois, certaines choses qui étaient vraies jusque-là ne le sont plus. Être confronté à des situations déstabilisantes liées à ces ruptures oblige à faire le tri de ce qui reste valide ou pas. Ce sont de belles occasions de débattre.
L’énoncé du débat
Lequel de ces deux nombres est le plus grand ?
NB : Le duo de nombres à comparer est à choisir en fonction du niveau de connaissances des apprenants. Il ne s’agit pas de proposer les trois comparaisons à la suite à un même public.
a) 99 ou 111 ?
b) 
ou 
?
c) 5,4 ou 5,333 ?
Quelques commentaires didactiques
Dans chacune des situations proposées, les écritures que l’on a sous les yeux peuvent être trompeuses.
a) Entre 99 et 111, le nombre le plus petit, 99, contient deux 9.
b) Entre et , les nombres de la deuxième fraction sont plus grands.
c) Entre 5,4 et 5,333, le deuxième nombre décimal est plus long.
On peut donc s’attendre aux réponses erronées suivantes.
a) 99 est plus grand que 111 car 9 est beaucoup plus grand que 1, et en plus ici il y a deux 9 contre seulement trois 1.
b) est plus grand que car les nombres 6 et 9 sont beaucoup plus grands que 2 et 3. Aussi, 6 parts, c’est plus que 2 parts.
c) 5,333 est plus long, c’est le plus grand. 333 est plus grand que 4, donc 5,333 est plus grand que 5,4.
Pour répondre correctement à la question posée, l’apprenant doit inhiber l’aspect visuel et se connecter au sens présent derrière les écritures. Cela ne peut se faire que s’il est capable de décoder ces écritures, notamment en mobilisant de bonnes images mentales des nombres ; d’où l’importance de les construire.
Dans tous les cas, le retour à un support matériel peut aider ; par la suite, l’apprenant sera invité à se réévoquer les matériels pour apprendre à s’en détacher. Une autre clé à utiliser en parallèle est le travail sur les équivalences numériques et leur verbalisation.
Détaillons ces idées pour chacune des comparaisons proposées.
a) Dans l’ensemble des nombres naturels, la compréhension de la numération passe aussi par la compréhension du fait que plus un nombre est “long”, c’est-à-dire plus il contient de chiffres, plus il est grand. Il n’est pas forcément intuitif a priori d’affirmer que peu importe ce qu’il y a comme « quantité » dans les rangs inférieurs, une seule entité du rang supérieur sera toujours plus grande. Réfléchir sur du matériel de numération avec lequel on peut faire des échanges d’un rang à l’autre peut aider, tout comme le fait de travailler avec des représentations mentales de celui-ci. Pour la comparaison de 99 et 111, une représentation avec du matériel de numération reconnecte au fait que dans 111, il y a une centaine, soit 10 dizaines (équivalence numérique), ce qui est plus grand que les 9 dizaines de 99 ; une réflexion du même type peut être menée pour comparer les 11 unités de 111 aux 9 unités de 99.
Illustration avec du matériel géométrique (matériel imagé issu de https://www.micetf.fr/numop/)
Quel est le plus grand nombre : 99 ou 111 ?
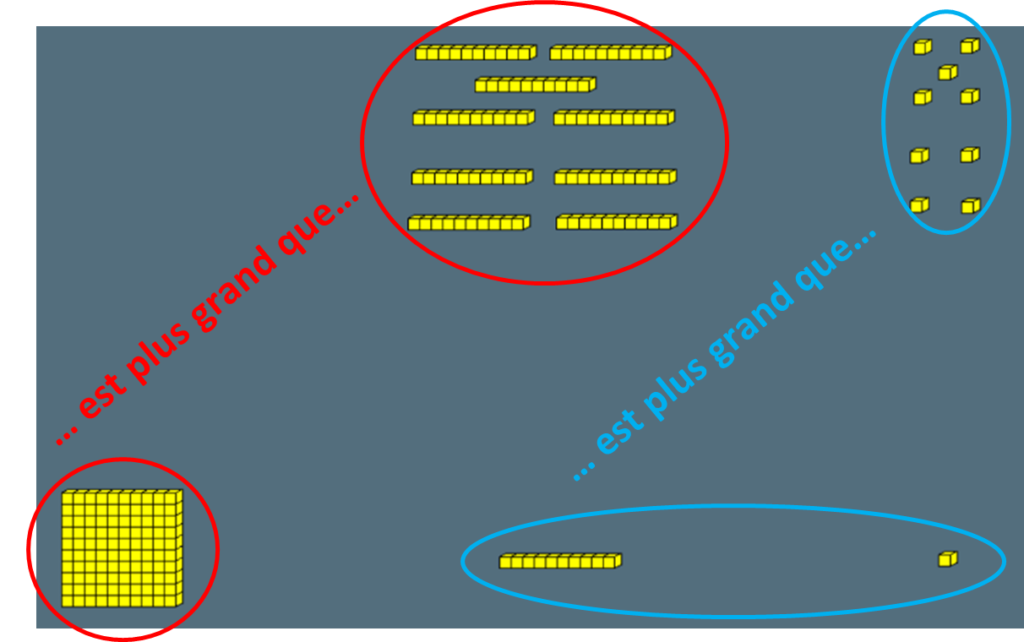
Pratiquer des échanges peut aider à se convaincre qu’une seule entité d’un rang sera toujours supérieure à l’ensemble des entités des rangs inférieurs.
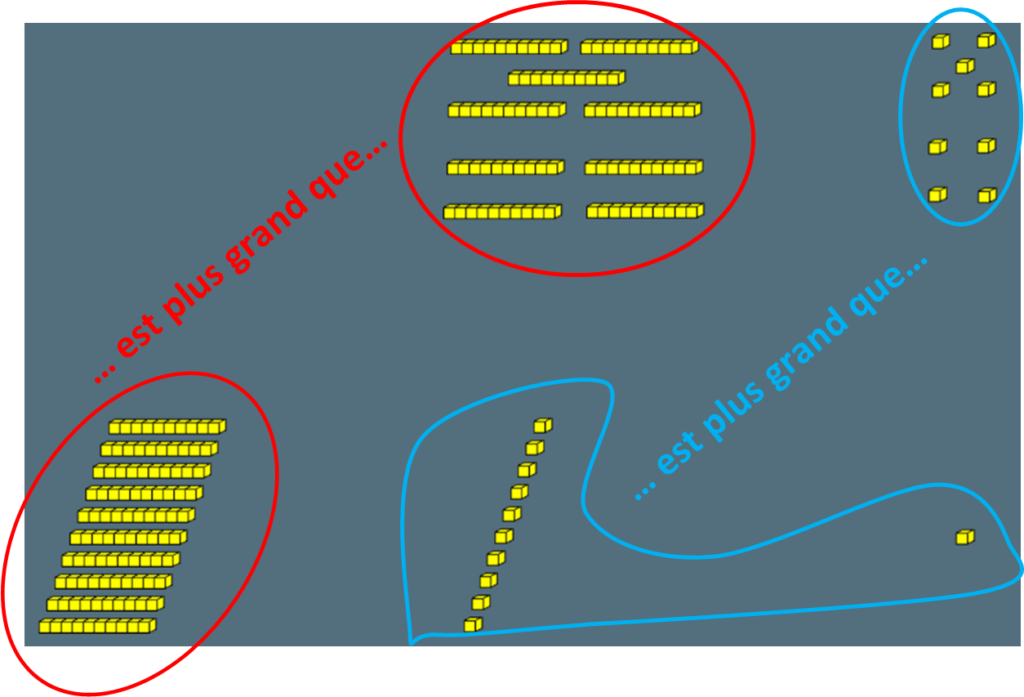
b) Pour la comparaison de et , d’un côté, fractionner par exemple un disque en trois parts égales et d’un autre, fractionner un disque identique en neuf parts égales. Dans le deuxième cas, on fait trois fois plus de parts (9 au lieu de 3), donc elles sont trois fois plus petites ; mais comme on en prend trois fois plus (6 au lieu de 2), cela revient au même. Un visuel qui pourrait s’avérer encore plus porteur est le fractionnement d’un rectangle en trois parties égales parallèlement à l’un de ses côtés d’abord, puis parallèlement à l’autre côté ensuite ; cette construction montre clairement les 3 neuvièmes dans chaque tiers.
 |  |
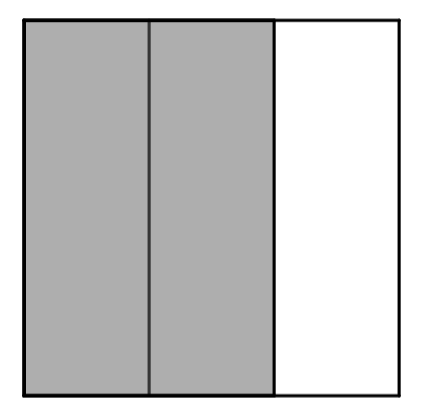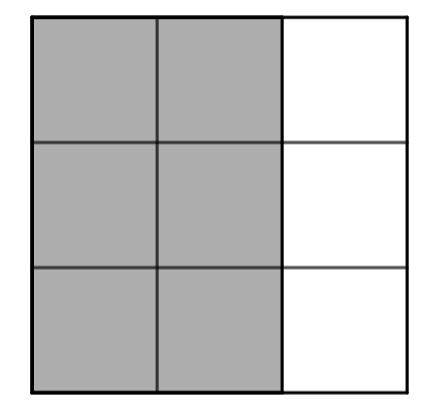Le matériel ExploRATIO proposé par le GEM met les apprenants au travail sur des tâches de ce type.
c) Contrairement à ce qui était vrai dans les naturels, lorsque deux nombres à virgule ont la même partie entière, ce n’est pas la longueur des parties décimales qui permet de les comparer. Pour comparer 5,4 et 5,333, si du matériel de numération (comme par exemple des pailles fractionnées) a été utilisé en support de la construction des rangs de la partie décimale, il peut être utilisé puis évoqué de la même façon qu’en a).
L’expression de l’équivalence numérique “4 dixièmes = 400 millièmes” et sa comparaison avec 333 millièmes devrait pouvoir être affirmée de manière solide par tous.
Au passage, on trouve donc de l’intérêt à lire 5,4 en disant “5 unités et 4 dixièmes” plutôt que “5 virgule 4” ainsi qu’à lire 5,333 en disant “5 unités et 333 millièmes” plutôt que “5 virgule 333” : l’oreille entend que l’on ne parle pas de la même chose (des dixièmes et des millièmes), ce qui peut inciter à la vigilance.
Échos d’une classe de P2
Comme dans tout débat, les enfants disposent d’un court temps de réflexion individuelle suivi d’un bref débat privé. L’objectif de celui-ci n’est pas de disposer d’une réponse commune, mais bien d’échanger des arguments ou même d’aider à se faire une idée d’une réponse. Puis, lors d’un vote en collectif, chaque enfant se positionne en faveur d’une des deux options : 99 ou 111. La réponse « je ne sais pas » est tolérée.
Ensuite, l’enseignante collecte les arguments.
« Il y a trois chiffres dans 111 et deux chiffres dans 99. » On pourrait se dire que le débat est plié… Eh bien non. Certains enfants tiennent à donner leur propre avis, sans être encore dans l’ouverture aux idées différentes des leurs qui pourraient faire évoluer leur pensée.
« 1+1+1 = 3 et 9+9 = 18 ; c’est 99 le plus grand. » Suite à cette intervention, deux enfants signifient qu’ils changent d’avis. Il est intéressant que l’enseignant pense à faire revoter à différentes reprises au fil du débat. Cela lui permet de voir évoluer les pensées, notamment celles des indécis.
« 99 est avant 100 et 111 est après 100 ; 111 est donc le plus grand. » C’est un point de vue ordinal qui est adopté par l’enfant qui fait cette proposition. C’est le cas aussi dans l’argument suivant : « Si on compte jusque 111, 99 est avant et 111 est après. »
« Dans 111, il y a une centaine, une dizaine et une unité. Dans 99, il y a seulement des dizaines et des unités. » On touche à l’argument-clef de la comparaison en cours, à savoir le nombre de rangs présents dans chaque nombre.
« Déjà, 9 est plus petit que 11… » On peut voir ici une stratégie de simplification, de décomplexification. L’enfant repart d’une comparaison similaire mais plus simple, et qu’il est capable de résoudre sans hésitation. C’est d’ailleurs cet argument qui fera changer d’avis les enfants qui s’appuyaient sur l’argument 9+9 > 1+1+1.
Il peut être intéressant de lister au tableau les arguments avancés. Tous les avis sont pris en compte, on peut identifier les ressemblances, les redondances, les divergences aussi.
Lors du vote final, tous les enfants de cette classe étaient tombés d’accord sur la bonne réponse ; ce n’est pas forcément toujours le cas. L’enseignante en a profité pour expliciter ce qui avait été appris comme stratégie pour comparer deux nombres naturels, avec un point d’attention sur une pratique inefficace, l’addition des chiffres des nombres à comparer. Ce temps d’institutionnalisation, le jour-même ou plus tard, est important pour que tous les enfants puissent sortir de la tempête d’idées provoquée par le débat et identifier ce qu’il en est ressorti.
Variantes dans l’univers des fractions
Les fractions regorgent de situations qui constituent des ruptures par rapport aux apprentissages qui précèdent. Chacune peut, au détour d’une hésitation et quel que soit l’âge des apprenants, générer un débat.
Relevons notamment ceci.
a) Comparer 
et 
.
Il faut deux nombres pour écrire une fraction, et ces deux nombres jouent des rôles différents.
b) Comparer 
et 
.
Comparer deux fractions, ce n’est pas comparer les nombres qui y apparaissent.
c) Voir le problème “Entre deux nombres” dans GEM (2017). Il met en lumière le fait que dans l’univers des fractions, la notion de successeur n’a plus de sens.
Références
ExploRATIO
https://www.micetf.fr/numop/
GEM (2017). Le plaisir de chercher en mathématiques. Louvain-la-Neuve : PUL.
Remerciements
Merci à Alicia et aux élèves de l’école fondamentale libre Saint-Joseph de Naast pour leur implication dans le débat présenté ici.