En manipulant les différents matériels, on fera apparaître une relation entre des angles ayant un sommet commun, d’autres entre les angles de certains quadrilatères et les conditions pour que ces relations existent.
Public : 10-12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
1. Déformer un pavage
Matériel 1
Des tiges métalliques fixées par des boulons afin de pouvoir déformer la construction

Matériel 2
Un cadre de quatre tiges métalliques fixées par des boulons auquel sont accrochés des fils élastiques qui font apparaître des parallélogrammes, des trapèzes ou des quadrilatères quelconques (l’élasticité des fils rend possible la déformation de la construction)

Activité
Pour chaque matériel,
a) déterminez les différents quadrilatères que l’on peut obtenir avec cette construction ;
b) pointez un angle du pavage ; modifiez son amplitude de 30° et observez comment varient les autres angles ; argumentez.
Solutions
a) Voici les différents quadrilatères que l’on peut obtenir.
Avec le matériel 1 : des rectangles et des carrés, des parallélogrammes et des losanges. Les rectangles se transforment en parallélogrammes, les carrés en losanges et inversement.

Avec le matériel 2 : des rectangles et des trapèzes. Les rectangles se transforment en parallélogrammes et inversement ; les trapèzes restent des trapèzes mais on passe de trapèzes rectangles à des trapèzes quelconques.

b) Avec le matériel 1, lorsqu’on modifie un angle de 30°, on voit que tous les angles de la construction varient de 30°. On s’en convainc sans avoir besoin de mesurer. Avec le matériel 2, lorsqu’on modifie un angle de 30°, les angles des parallélogrammes varient de 30°. Par contre, pour les trapèzes, seuls deux angles varient de 30° (les angles adjacents aux parallélogrammes). Il n’est pas évident de voir qu’il n’en est pas de même pour les deux autres angles, mais on peut le vérifier de diverses façons (mesure, découpe d’angles).
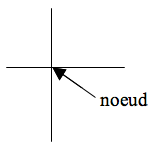
Pour les deux matériels, si on observe quatre angles situés à un « nœud » du pavage, on voit que les angles opposés par leur sommet varient de manière identique.
2. Déformer un quadrilatère
Matériel 1
Des tiges métalliques fixées par des boulons afin de pouvoir déformer la construction (tiges formant un rectangle, un carré ou un trapèze)

Matériel 2
Des tiges métalliques fixées par des boulons (auxquels un disque gradué transparent est attaché) afin de pouvoir déformer la construction (tiges formant un rectangle, un carré ou un trapèze)


Activité
Pour chaque matériel,
a) déterminez les différents quadrilatères que l’on peut obtenir avec cette construction,
b) choisissez un angle. Modifiez son amplitude de 30° et observez comment varient les autres angles; argumentez.
Solutions
En déformant un carré, on obtient des losanges ; en déformant un rectangle, on obtient des parallélogrammes ; en déformant un trapèze, on obtient des quadrilatères quelconques.
Pour visualiser la déformation des quadrilatères articulés, bougez le point Mob ou certains autres sommets du quadrilatère. Vous pouvez aussi modifier les longueurs des tiges.
En travail inverse, en déformant un losange, on obtient des losanges et à un « moment » un carré ; en déformant un parallélogramme on obtient des parallélogrammes et à un « moment » un rectangle.
Le matériel 2 permet d’exprimer qu’en chaque sommet il y a 360° et qu’en chaque sommet, un angle obtus et un angle aigu forment ensemble un angle de 180°.
Lorsque les tiges sont de même longueur deux à deux, elles sont forcément parallèles et, si on augmente l’amplitude d’un angle de 30°, les amplitudes des autres angles augmentent ou diminuent de 30°.
3. Retrouver des angles de même amplitude dans un pavage
Activité
Coloriez dans une même couleur, sans instrument de mesure, tous les angles de même amplitude.
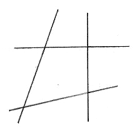
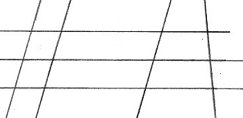
Quelles régularités observes-tu ? Quand n’est-ce pas régulier ?
Aide
Comment aider l’élève qui ne voit pas que le nœud se répète ?
Si on travaille avec un matériel (treillis de tiges articulées ou cadre en tiges articulées et treillis en élastique), on photocopie la construction.
Si on travaille sur un treillis dessiné, on donne un nouvel exemplaire.
Découper un morceau du treillis pour isoler un nœud ou décalquer un nœud.
Proposer à l’élève de superposer le nœud découpé ou décalqué aux autres nœuds.
Solutions

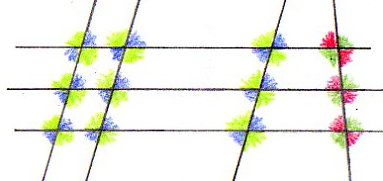
Dans les deux constructions, à chaque nœud, on a :
- quatre angles ;
- deux angles aigus et deux angles obtus qui se suivent en alternance, aigu,obtus, aigu, obtus ;
- la somme des quatre angles est égale à 360° ;
- deux angles qui se suivent (consécutifs) forment un angle plat ;
- si on modifie l’amplitude d’un angle, l’amplitude de tous les autres est modifiée ;
- les angles opposés par leur sommet ont la même amplitude.
Dans la 2e construction :
On a les régularités suivantes pour les angles formés par les droites parallèles. Elles n’apparaissent pas sur les nœuds qui se trouvent sur la droite qui n’est pas parallèle aux autres.
- Si on modifie l’amplitude d’un des angles, toutes les autres sont modifiés. Ce qu’un angle perd en amplitude est gagné par l’angle suivant.
- Chaque nœud se répète par glissement (on observe en chaque nœud des angles de même amplitude).
- Dans tous les parallélogrammes, les angles intérieurs opposés ont la même amplitude.
Ceci qui suit peut également ressortir de l’observation. Dans ce cas l’activité 4 n’a plus lieu d’être.
- Dans chaque parallélogramme, la somme des amplitudes des angles est égale à 360°.
- Dans chaque parallélogramme, la somme des amplitudes de deux angles consécutifs est égale à 180°.
4. Somme des amplitudes des angles intérieurs dans un parallélogramme
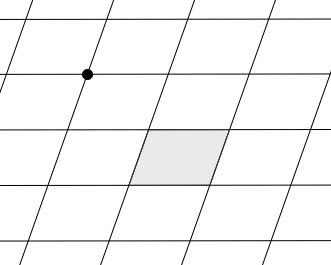
Activité
1. Autour du nœud mis en gras, repère les angles de même amplitude et colorie-les d’une même couleur.
2. Dans le parallélogramme grisé, repère les angles qui ont la même amplitude que ceux que tu viens de colorier. Colorie-les en utilisant les mêmes couleurs.
3. Sans utiliser de rapporteur, détermine la somme des amplitudes des angles intérieurs du parallélogramme.
Aide
Comment aider l’élève à voir que la somme des angles intérieurs d’un parallélogramme est égale à 360° ?
Donner un deuxième exemplaire.
Découper les angles autour du nœud de telle sorte que chaque angle soit isolé.
Proposer à l’élève de superposer les angles découpés aux angles intérieurs du parallélogramme.
Solutions

– Dans chaque parallélogramme, la somme des amplitudes des angles est égale à 360°.
– Dans chaque parallélogramme, la somme des amplitudes de deux angles consécutifs est égale à 180°.
Activités en amont
Activités en aval
Contenus visés
- Relation entre les angles dans un parallélogramme
- Somme des amplitudes des angles dans un triangle
Instruments de pensée
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|

