Ces activités permettent de travailler l’instrument de pensée composer-décomposer tout en (re)découvrant quelques quadrilatères et en établissant des liens entre figures.
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
À partir d’un rectangle
Voici un rectangle. On en dispose de plusieurs copies.

Découpez-le en deux morceaux puis assemblez ceux-ci pour obtenir un autre quadrilatère. Réfléchissez avant à la façon dont vous allez découper le rectangle.
Faites un dessin de votre assemblage.
Ensuite trouvez d’autres découpages et assemblages pour obtenir d’autres quadrilatères bien différents à partir de copies de ce même rectangle. Dessinez les figures que l’on peut ainsi obtenir.
Solutions
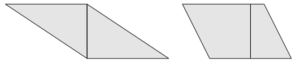
On peut classer les quadrilatères selon leurs propriétés habituelles et leur donner des noms. On trouve des parallélogrammes.
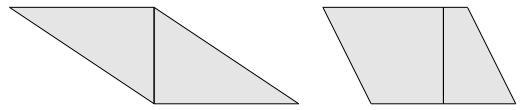
Et parmi eux, un losange (qu’on ne s’attend pas à trouver parmi les productions des enfants).
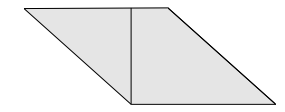
Mais aussi des trapèzes isocèles, des trapèzes rectangles.
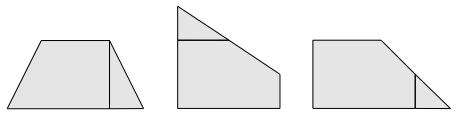
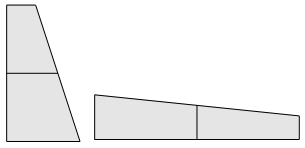
Ainsi que deux rectangles.
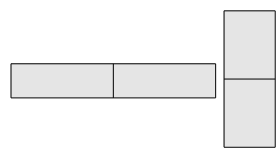
Et un cerf-volant.
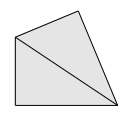
À partir d’un carré

Voici un carré. On ne dispose que d’une seule copie.
Découpez-le en deux morceaux pour pouvoir obtenir, par assemblage de ces deux morceaux, un parallélogramme (non rectangle), un trapèze (non parallélogramme), un triangle et un autre quadrilatère. Réfléchissez avant à la façon dont vous allez découper le carré pour pouvoir faire tout cela avec les deux mêmes morceaux.
Solutions
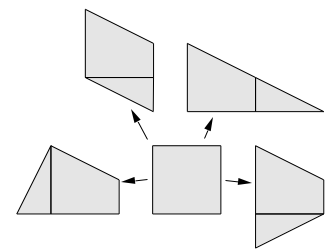
Partage de même aire
Voici un carré.

a) En traçant des traits à partir du centre, découpez-le en 12 parts d’aires égales.
b) Même consigne pour 6 parts d’aires égales. Justifiez votre construction.
Solutions
On peut d’abord penser à partager le carré en 4 parts égales suivant ses diagonales. Les quatre triangles ont même aire par symétrie. Cela se voit.

On peut ensuite couper chaque triangle en trois parts de même aire : il suffit de couper leur base en trois parts égales pour obtenir des triangles de même base et de même hauteur, donc de même aire.
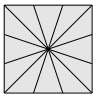
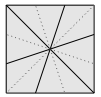
Pour partager le carré en 6 parts égales, il suffit de grouper les petits triangles deux par deux.
Activités en amont
Activités en aval
Contenu visé
- Application des formules d’aire du triangle
Instruments de pensée
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|