Public : 12 – 14 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Activité 1 : Créer une famille de triangles d’aires égales
a) Trouve un point C pour que le triangle ABC ait une aire de 12,5 cm².
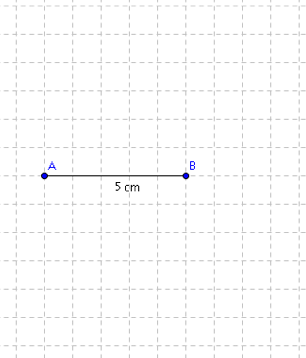
b) Sur la même figure, trouve tous les points C pour que le triangle ABC ait une aire de 12,5 cm².
Solution
La hauteur doit mesurer 5 cm. Voici quelques solutions :
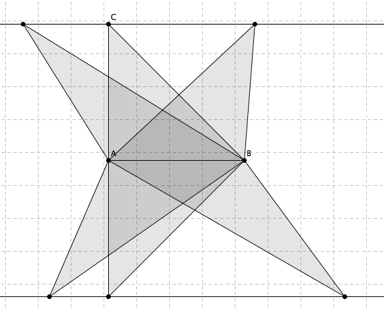
L’ensemble de tous les points C qui conviennent est constitué de deux droites parallèles à la base [AB].
Conclusion : si deux triangles ont la même base et les sommets opposés à cette base sur une droite parallèle à celle-ci, alors ils ont la même aire.
Activité 2 : Famille de triangles de même aire
Sans calculer, sans mesurer, tracez plusieurs triangles de même aire que ABC.

Solutions
Une méthode possible consiste à garder la base du triangle et à « pousser » le sommet opposé sur une parallèle à la base.
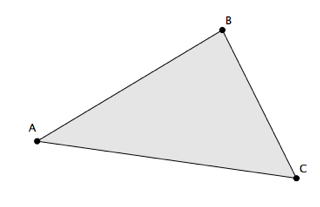
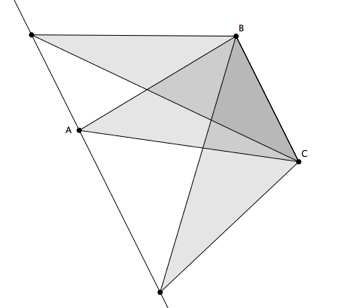
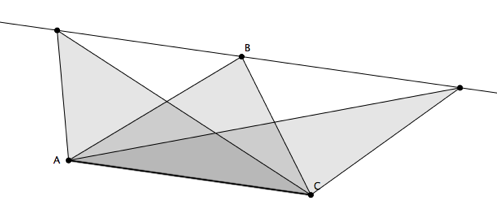
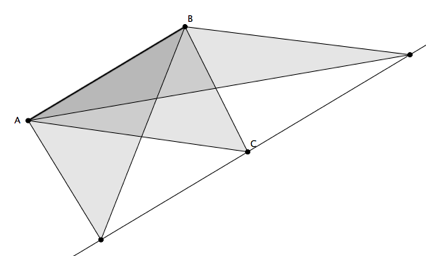
On peut engendrer plusieurs familles de triangles en réitérant le processus…
Activité 3 : Quadrupler l’aire d’un triangle
Une méthode possible consiste à garder la base du triangle et à « pousser » le sommet opposé sur une parallèle à la base.
On peut engendrer plusieurs familles de triangles en réitérant le processus…
En déplaçant un ou deux sommets, quadruplez l’aire du triangle ABC.
Trouvez plusieurs manières bien différentes d’y parvenir.
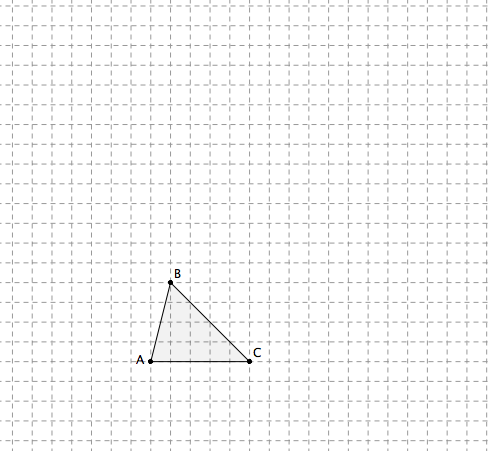
Solutions
Voici quatre procédés pour quadrupler l’aire du triangle.
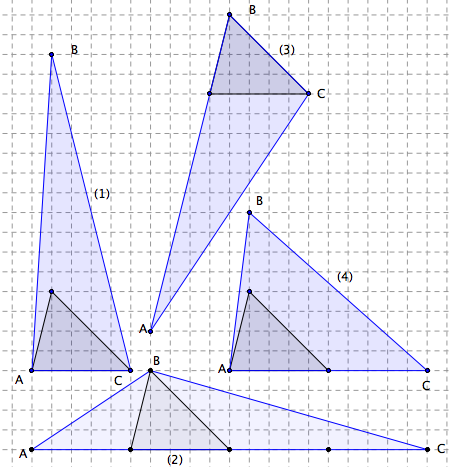
En (1), on a quadruplé la hauteur. En (2), c’est la base qui est quadruplée.
On utilise les propriétés suivantes :
– le rapport des aires de deux triangles de même base est égal au rapport de leurs hauteurs,
– le rapport des aires de deux triangles de même hauteur est égal au rapport de leurs bases.
Le procédé (3) se base aussi sur cette dernière propriété, mais c’est un autre côté qui a été choisi comme base.
On peut aussi, comme en (4), choisir de doubler la base — l’aire est ainsi doublée — puis de doubler la hauteur — l’aire est ainsi à nouveau doublée, donc quadruplée au total.
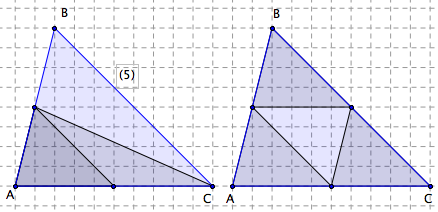
En (5), on a doublé une base, puis une autre. La dernière figure montre que, dans le grand triangle ainsi obtenu, on peut placer quatre triangles isométriques au triangle de départ. Remarquons que le grand triangle est un agrandissement (une figure semblable) du petit.
Activité 4 : Comparer des aires de triangles
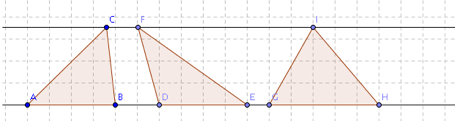
a) Comparez les aires des triangles ABC, DEF et GHI.
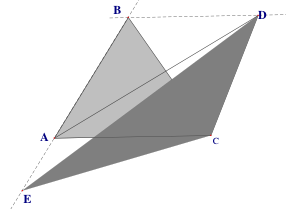
b) Comparez les aires des triangles ABC, ADC, EDC.
Solutions
a) Les triangles ABC et DEF ont même base et même hauteur donc même aire. Le triangle GHI a aussi même hauteur mais une plus grande base, donc une aire plus grande.
b) Deux triangles de même base et dont les troisièmes sommets sont sur une parallèle à leur base commune ont même aire : les triangle ABC et ADC ont donc même aire. Par contre les points A et E ne sont pas sur une même droite parallèle à DC. La hauteur de EDC relative à la base [DC] est plus grande que celle de ADC relative à la même base. Le triangle EDC a une aire plus grande que ADC et ABC.
Activités en amont
- Aires de triangles à 10-12 ans
- Dissections géométriques à 10-12 ans
- Familles de triangles à 12-14 ans
Activités en aval
- Partages d’aires à 12-14 ans
Instruments de pensée
- Changement de point de vue
- Mouvement et déformation de figures
- Évoquer une situation intermédiaire
Contenu visé
- Formules d’aires de quelques figures planes
- Ce contenu intervient dans la démonstration du théorème de Thalès par les aires de triangles et dans la démonstration du théorème de Pythagore par les aires des triangles.
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|

