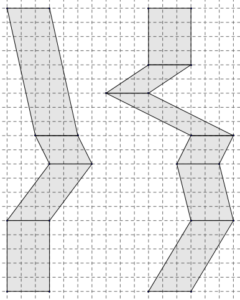
Cette suite d’activités a pour objectif de réinvestir les connaissances sur les aires des parallélogrammes. Elle permet de développer ou de renforcer des instruments de pensée, tels le mouvement, le découpage-assemblage et le changement de point de vue.
Bien que la formule soit déjà vue, son utilisation n’est pas automatique. Par ailleurs, les élèves peuvent se passer de la formule et travailler par mouvement, découpage…
Public : 10 – 12 ans
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|
Activité 1
Voici deux « trains de parallélogrammes ». Sans rien mesurer ni calculer, compare leurs aires.
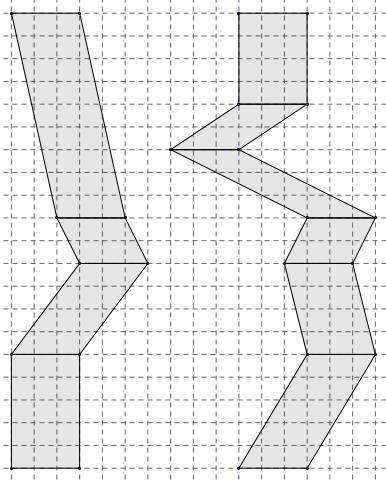
Pistes
Remarquer qu’il est plus facile de commencer la comparaison des trains par le bas de la figure.
Les comparaisons peuvent se faire par « étage ».
On peut, au choix, transformer les parallélogrammes en rectangles de même aire,
– par découpage,
– en évoquant une déformation qui conserve l’aire,
– en évoquant directement la formule d’aire du parallélogramme.
On peut, si nécessaire, demander comment on s’y prendrait pour calculer l’aire du parallélogramme et du rectangle du premier étage (en bas).
Solutions
Des enfants pourraient commencer par compter un à un les carrés entiers contenus dans les trains, puis essayer d’assembler les morceaux de carrés. Il vaut mieux les encourager à comparer plus globalement les figures et à appliquer leur idée de ce découpage-assemblage aux parallélogrammes eux-mêmes.
Voici quelques démarches possibles pour résoudre ce problème.
1. On peut partir du bas, du 1er étage, se ramener du parallélogramme au rectangle par découpage, et ainsi de suite pour les trois premiers étages.
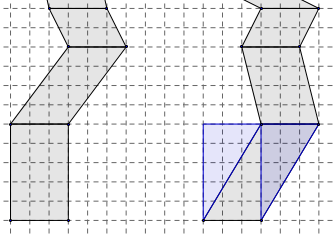
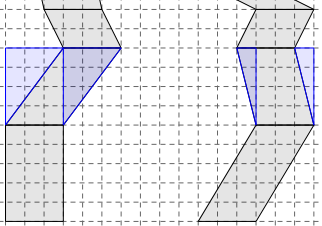
2. Pour le troisième étage, on peut évoquer la symétrie : les deux parallélogrammes sont superposables par retournement.
3. On peut également évoquer le fait que l’aire d’un parallélogramme dépend de sa base et de sa hauteur. Or pour les trois premiers étages, les bases sont égales et les hauteurs correspondantes aussi.
4. Si on veut comparer les deux trains, étage par étage, le problème des parallélogrammes du haut est plus délicat. On peut alors décomposer le grand parallélogramme de gauche en trois parties et appliquer la même méthode que pour les parallélogrammes du bas. La difficulté ici est que les extrémités des deux nouveaux côtés horizontaux ne sont pas des nœuds du quadrillage.
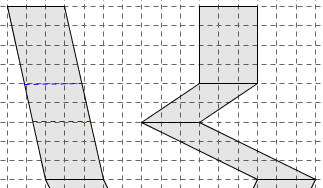
5. On peut aussi s’abstenir de comparer les parallélogrammes par étage, mais plutôt pour chaque train, transformer successivement tous les parallélogrammes en rectangles, par découpage.
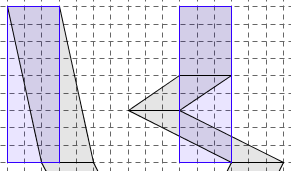
6. Enfin, on peut déformer chaque train de parallélogrammes en un grand rectangle.
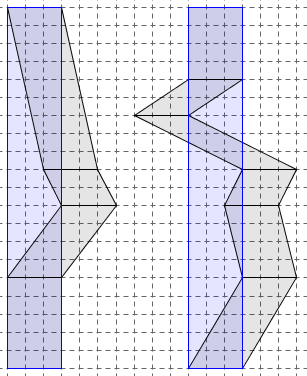
Activité 2
Combien de petits carrés contient chaque train de parallélogrammes ?
Solutions
Voici quelques démarches possibles pour résoudre ce problème.
On peut se ramener directement à un rectangle. On voit alors que l’aire contient 3 x 20 carrés.
Mais on peut aussi calculer séparément l’aire de chaque parallélogramme, puis additionner. On obtient
3 x 5
+ 3 x 4
+ 3 x 2
+ 3 x 9 =
= 15 + 12 + 6 + 27 = 60.
Si les élèves ont travaillé des techniques de calcul faisant intervenir la distributivité, ils pourraient remarquer le facteur commun et calculer directement 3 x (5+4+2+9) = 3 x 20. Ceci peut être mis en relation avec la première démarche.
Activité 3
Parmi les trains suivants, quel est celui de plus grande aire ? Celui de plus petite aire ?
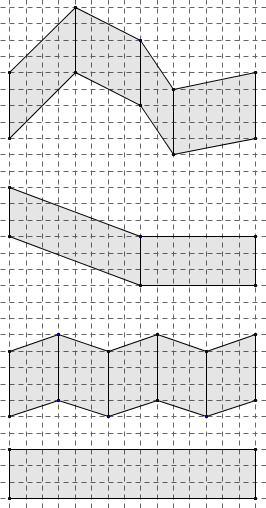
Solutions
L’idée n’est pas de « faire du drill » sur ce type d’activité mais de permettre à certains de s’approprier les démarches empruntées en les réinvestissant dans une situation de la même famille. La situation est un peu différente : les côtés communs sont verticaux et ils ne sont pas tous de même longueur.
On a intérêt à considérer les bases verticales et les hauteurs horizontales. Les quatre hauteurs sont alors égales mais non les bases. Les premier et troisième trains ont même aire, ainsi que le deuxième et le quatrième qui ont une aire plus petite que la précédente.
Activité 4
Composez deux trains de parallélogrammes ayant même aire.
Solutions
Selon la production des élèves, on peut exploiter l’un ou l’autre dessin, original, juste ou faux, pour faire réagir les autres élèves.
Activités en amont
- Aire des parallélogrammes
- Familles de parallélogrammes à 10-12 ans
- Comparaison et déformation de figures à 10-12 ans
Activités en aval
Instruments de la pensée géométrique
- Changement de point de vue
- Mouvement et déformation de figures
- Évoquer une situation intermédiaire
- Composer-décomposer
| Retour au tableau d’accueil Une géométrie articulée de 10 à 15 ans |
|---|